Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 2.Exercícios - Ex. 14
Uma empresa de eletricidade oferece uma taxa vitalícia de energia a qualquer lar cuja utilização de energia esteja abaixo de durante um determinado mês. Represente por o evento de um lar selecionado aleatoriamente em uma comunidade que não excede a utilização da taxa vitalícia em janeiro e por o evento análogo para o mês de julho ( e se referem ao mesmo lar). Suponha que Calcule
a. .
b. A probabilidade de a quantia da taxa vitalícia ser excedida em exatamente um dos dois meses. Descreva esse evento em termos de e .
Passo 1
a.
então
Passo 2
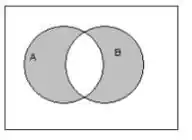
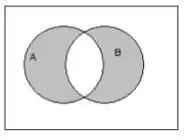
b. região sombreada
região sombreada evento de interesse
Resposta
Exercícios de Livros Relacionados
Considere o lançamento de dois dados. Considere os eventos: A = soma dos números obtidos igual a 9, e B = número no primeiro dado maior ou igual a 4. Enumere os elementos de A e B. ObtenhaA ∪ B ,A ∩ B
Prove que, se A e B são independentes, também o serão Ac e Bc, A e Bc e Ac e B.
Na figura abaixo temos um sistema chamado ponte. Nas mesmas condições do Problema 22, obtenha a confiabilidade do sistema.
Considere, agora, a situação do Problema 49, mas suponha que o quadrado não tenha área unitária. Como você definiria a probabilidade de um evento A?
No Problema 2, suponha que 5 indique o aparecimento da face 5 e Q indique que apareceu outra face qualquer diferente da 5. Atribua probabilidade (5/6)k (1/6) a cada ponto com k letras iguais a Q segui