Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 5.Problemas - Ex. 12

Considere o lançamento de dois dados. Considere os eventos: A = soma dos números obtidos igual a 9, e B = número no primeiro dado maior ou igual a 4. Enumere os elementos de A e B. Obtenha   A ∪ B ,   A ∩ B ,   A c .

Passo 1

Primeiramente, vamos escrever nosso espaço amostral.

Ao lançarmos dois dados temos 6 × 6 = 36 possíveis resultados. Seja ( i , j ) o resultado em i do dado 1 e de j do dado 2.

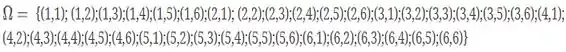
Passo 2

Seja o evento A a soma dos números obtidos igual a 9.

A = { 3,6 ; 4,5 ; 5,4 ; 6,3 }

Passo 3

Seja o evento B igual a todas as combinações cujo o número no primeiro dado seja maior ou igual a 4.

B = { 4,1 ; 4,2 ; 4,3 ; 4,4 ; 4,5 ; 4,6 ; 5,1 ; 5,2 ; 5,3 ; 5,4 ; 5,5 ; 5,6 ; 6,1 ; 6,2 ;

                        6,3 ; 6,4 ; 6,5 ; ( 6 , 6 ) }

Passo 4

Agora que já conhecemos quem são os conjuntos, vamos calcular:

i A ∪ B

i i A ∩ B

i i i A c

Passo 5

Calculando i A ∪ B :

Basta unir os conjuntos, ou seja, os elementos que forem que diferentes devem ser adicionados e os repetidos só devem ser contados uma única vez.

A ∪ B = { 3,6 ; 4,1 ; 4,2 ; 4,3 ; 4,4 ; 4,5 ; 4,6 ; 5,1 ; 5,2 ; 5,3 ; 5,4 ; 5,5 ; 5,6 ;

                                                6,1 ; 6,2 ; 6,3 ; 6,4 ; 6,5 ; ( 6,6 ) }

Passo 6

Calculando i i A ∩ B :

Para calcular a interseção, basta verificar quais elementos são comuns aos dois eventos.

A ∩ B = { 4,5 ; 5,4 ; 6,3 }

Passo 7

Calculando i i i A c :

Resposta

A = { 3,6 ; 4,5 ; 5,4 ; 6,3 }

B = { 4,1 ; 4,2 ; 4,3 ; 4,4 ; 4,5 ; 4,6 ; 5,1 ; 5,2 ; 5,3 ; 5,4 ; 5,5 ; 5,6 ; 6,1 ; 6,2 ;

                        6,3 ; 6,4 ; 6,5 ; ( 6,6 ) }

A ∪ B = { 3,6 ; 4,1 ; 4,2 ; 4,3 ; 4,4 ; 4,5 ; 4,6 ; 5,1 ; 5,2 ; 5,3 ; 5,4 ; 5,5 ; 5,6 ;

                                                6,1 ; 6,2 ; 6,3 ; 6,4 ; 6,5 ; ( 6,6 ) }

A ∩ B = { 4,5 ; 5,4 ; 6,3 }

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma classe de estatística teve a seguinte distribuição das notas finais: 4 do sexo masculino e 6 do sexo feminino foram reprovados, 8 do sexo masculino e 14 do feminino foram aprovados. Para um aluno
Uma classe de estatística teve a seguinte distribuição das notas finais: 4 do sexo masculino e 6 do sexo feminino foram reprovados, 8 do sexo masculino e 14 do feminino foram aprovados. Para um aluno
Uma classe de estatística teve a seguinte distribuição das notas finais: 4 do sexo masculino e 6 do sexo feminino foram reprovados, 8 do sexo masculino e 14 do feminino foram aprovados. Para um aluno
Uma classe de estatística teve a seguinte distribuição das notas finais: 4 do sexo masculino e 6 do sexo feminino foram reprovados, 8 do sexo masculino e 14 do feminino foram aprovados. Para um aluno
Num experimento, 15 coelhos foram alimentados com uma nova ração e seu peso avaliado ao fim de um mês. Os dados referentes ao ganho de peso (em quilogramas) foram os seguintes: 1,5 ; 1,6 ; 2,3 ; 1,7 ;