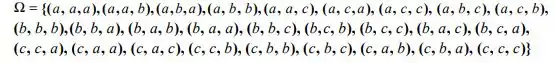Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 5.Problemas - Ex. 43
Numa empresa existem operários de determinada categoria, com idades iguais a a, b e c anos (existem pelo menos três com a mesma idade). Escolhem-se três ao acaso para que façam determinado curso. Se indicarmos por x a idade do primeiro, y a do segundo e z a do terceiro, o terno (x, y, z) indica cada possível resultado. Enumere:
(a) o espaço amostral; e (b) os eventos A = {(x, y, z)|x = y = z}, B = {(x, y, z)|x = y}.
Passo 1
(a) o espaço amostal.
Representando o espaço amostral por , temos
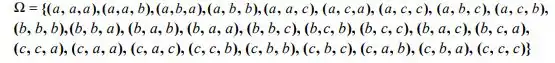
Passo 2
(b) os eventos A = {(x, y, z)|x = y = z}.
Ou seja, queremos a idade primeiro, do segundo e do terceiro, TAL QUE, a idade do primeiro, do segundo e do terceiro SEJAM IGUAIS.
Passo 3
os eventos B = {(x, y, z)|x = y}.
Ou seja, queremos a idade primeiro, do segundo e do terceiro, TAL QUE, a idade do primeiro e do segundo SEJAM IGUAIS. Como não há restrição para a idade do terceiro, ela pode ser igual ou não.
Resposta
