Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 5.Problemas - Ex. 34

Um empreiteiro apresentou orçamentos separados para a execução da parte elétrica e da parte de encanamento de um edifício. Ele acha que a probabilidade de ganhar a concorrência da parte elétrica é de 1/2. Caso ele ganhe a parte elétrica, a chance de ganhar a parte de encanamento é de 3/4; caso contrário, essa probabilidade é de 1/3. Qual a probabilidade de ele:

(a) ganhar os dois contratos?

(b) ganhar apenas um?

(c) não ganhar nada?

Passo 1

Eta! Temos muitas informações, né? Vamos começar nomeando os eventos para nos organizarmos melhor:

E G = g a n h a r   a   p a r t e   e l é t r i c a

E P = p e r d e r   a   p a r t e   e l é t r i c a

C G = g a n h a r   a   p a r t e   d e   e n c a n a m e n t o

C P = p e r d e r   a   p a r t e   d e   e n c a m a n e n t o

Agora vamos tentar escrever o enunciado através de um diagrama?

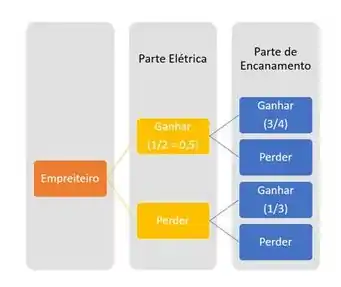
Passo 2

Vamos completar esse diagrama com as probabilidades que faltam?

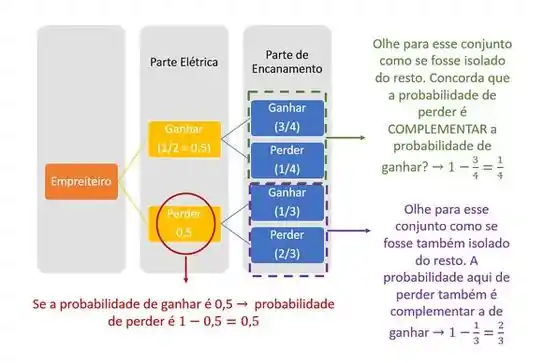
Passo 3

Agora temos a probabilidade de cada etapa, certo? Mas, você sabe o que cada parte significa?

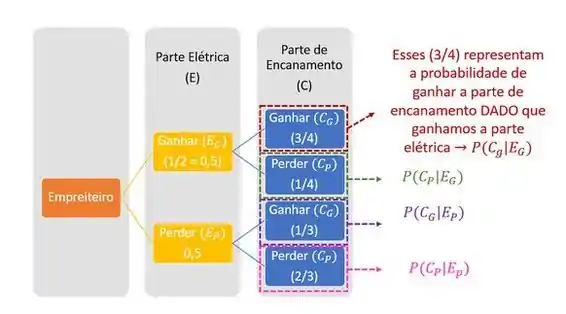
Beleza?

Passo 4

Agora que já entendemos direitinho o diagrama, vamos olhar para o que a questão pede:

(a) Qual a probabilidade de ele ganhar os dois contratos?

Isso quer dizer: P E G ∩ C G

Bom, sabemos que

P E G = 0,5

P C G E G = 3 4

Lembrando da fórmula da condicional, temos:

P C G E G = P E G ∩ C G P E G → P E G ∩ C G = P C G E G . P ( E G )

Substituindo

P E G ∩ C G = 3 4 . 1 2 = 3 8 = 0,375

Passo 5

(b) Qual a probabilidade de ele ganhar apenas um?

Bom, para ele ganhar apenas um temos duas situações:

i Ganhar a parte elétrica e perder a parte do encamento ou

( i i ) Perder a parte elétrica e ganhar a parte do encanamento

Vamos calcular a probabilidade de cada um e somar, ok?

Passo 6

i Ganhar a parte elétrica e perder a parte do encamento P ( E G ∩ C P )

Vamos usar o mesmo raciocínio da alternativa (a)!

Sabemos que

P E G = 0,5

P C P E G = 1 4

Pela fórmula da probabilidade condicional, temos:

P C P E G = P E G ∩ C P P E G → P E G ∩ C P = P C P E G . P ( E G )

P E G ∩ C P = 1 4 . 1 2 = 1 8

Passo 7

i i Perder a parte elétrica e ganhar a parte do encamento P ( E P ∩ C G )

Sabemos que

P E P = 0,5

P C G E P = 1 3

Pela fórmula da probabilidade condicional, temos:

P C G E P = P E P ∩ C G P E P → P E P ∩ C G = P C G E P . P ( E P )

P E P ∩ C G = 1 3 . 1 2 = 1 6

Passo 8

Somando ( i ) e ( i i ) , temos:

1 8 + 1 6 = 7 24 ≅ 0,292

Passo 9

Isso não tem fim? Prometo que esse será o nosso último passo 😉.

(c) Qual a probabilidade de ele não ganhar nada?

Probabilidade de não ganhar nada Perder a parte elétrica e perder a parte de encanamento P ( E P ∩ C P )

Sabemos que

P E G = 0,5

P C P E P = 2 3

Usando mais uma vez a fórmula da probabilidade condicional, temos:

P C p E P = P E P ∩ C P P E P → P E P ∩ C P = P C P E P . P ( E P )

P E P ∩ C G = 2 3 . 1 2 = 1 3 ≅ 0,333

UFA! ACABAMOS!

Resposta

a   0,375

b   ≅ 0,292

c   ≅ 0,333

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual é a probabilidade de que pelo menos um de um par de dados honestos caia no 6, dado que a soma dos dados seja i, i = 2, 3, ... ,12?
Use a Equação (2.1) para calcular, em uma mão de bridge, a probabilidade condicional de que Leste tenha 3 espadas dado que Norte e Sul tenham um total combinado de 8 espadas.
Um casal tem duas crianças. Qual é a probabilidade de que ambas sejam meninas se a mais velha das duas crianças for uma menina?
Uma urna contém 6 bolas brancas e 9 bolas pretas. Se 4 bolas devem ser selecionadas aleatoriamente sem devolução, qual é a probabilidade de que as 2 primeiras bolas selecionadas sejam brancas e as 2 ú
Se dois dados honestos são rolados, qual é a probabilidade condicional de que o primeiro caia no 6 se a soma dos dados é i? Calcule essa probabilidade para todos os valores de i entre 2 e 12.