Numa empresa, as importações de uma certa matéria-prima (em milhões de toneladas), no período 1969/1975, estão mostradas na tabela abaixo:

Foi adotada a escala de tempo acima mostrada e foram calculados os somatórios necessários para montagem de uma regressão linear simples, obtendo:

Pede-se:

1. Qual a estimativa do decréscimo anual dessas importações?
2. Para que ano espera-se que essas importações reduzam-se para 30.000.000 toneladas?
3. Testar a existência da regressão linear simples, ao nível de , e calcular o poder de explicação.

Então vamos lá para nosso exercício, do enunciado temos os seguintes dados:

E no item a) queremos descobrir o decréscimo anual das importações, então queremos descobrir o valor de . Primeiro iremos calcular as médias de e de , respectivamente:

E as variâncias:

Com esses valores calculados, conseguimos calcular o valor de :

Ou seja, o decréscimo anual será de 9,46 milhões de toneladas.

Para item b) iremos precisar da equação da reta, para isso precisamos calcular o valor de :

Gerando a equação:

Para descobrirmos o ano que as importações irão reduzir para 30.000.000 toneladas, iremos considerar que :

Arredondando para o próximo número redondo:

Aumentando os valores de até 8:

O ano será por volta de 1980.

No item c) queremos testar a existência da regressão linear simples. Então iremos testar através do estudo da Análise de Variância e do Coeficiente de Explicação, onde:

Se , existe a regressão de sobre .

E o coeficiente de explicação é calculado por:

Então primeiro iremos calcular os graus de liberdade para encontrarmos nosso valor de tabelado:

• ;
• ;
• .

Para , nosso será:

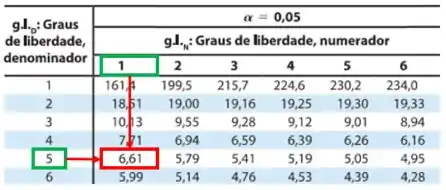
Agora vamos calcular as somas dos quadrados:

Como (), então existe regressão.

E por fim, conseguimos encontrar o coeficiente de explicação:

Esse já acabou pessoal. Te espero em mais exercícios.