Encontrando probabilidades. Use a distribuição de probabilidades que você construiu no Exercício 19 para encontrar a probabilidade de selecionar aleatoriamente um domicílio que tenha
(a) um ou dois televisores
Passo 1
Precisamos calcular as probabilidades associadas a quantidade de domicílios em relação ao seu total. Sendo X a variável aleatória discreta o número de televisores por domicílio em uma cidade pequena, temos:
Passo 2
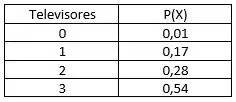
Sendo assim, a tabela de distribuição de probabilidades para letra (a) fica:
Passo 3
O “ou” na matemática significa soma. Neste caso, para podermos encontrar a probabilidade de selecionar aleatoriamente um domicílio que tenha um ou dois televisores, temos que somar as probabilidades dos domicílios que tenham um ou dois televisores em casa: