Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Probabilidade, um curso moderno com aplicações, de Sheldon Ross- Ed: 8º - Capítulo 3.Problemas - Ex. 52

Uma estudante de segundo grau aguarda ansiosamente o recebimento de uma carta dizendo se ela foi aceita ou não em determinada faculdade. Ela estima que as probabilidades condicionais de receber a carta de notificação em cada um dos dias da próxima semana, dado que ela tenha sido aceita ou rejeitada, sejam as seguintes:

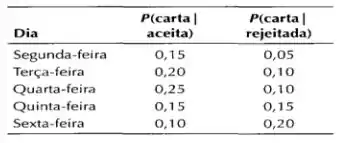
Ela estima que sua probabilidade de ser aceita seja de 0,6.

(a) Qual é a probabilidade de que ela receba a carta na segunda?

(b) Qual é a probabilidade de que ela receba a carta na terça dado que ela não tenha recebido uma carta na segunda?

(c) Se nenhuma carta chegar até a quarta-feira, qual é a probabilidade condicional de que ela tenha sido aceita?

(d) Qual é a probabilidade condicional de que ela seja aceita se a carta chegar na quinta?

(e) Qual é a probabilidade condicional de que ela seja aceita se nenhuma carta chegar naquela semana?

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Primeiro, vamos identificar os eventos, temos os seguintes eventos:

A - E l a   f o i   a c e i t a

M - E l a   r e c e b e   a   n o t i f i c a ç ã o   n a   S e g u n d a

T -   E l a   r e c e b e   a   n o t i f i c a ç ã o   n a   T e r ç a

W -   E l a   r e c e b e   a   n o t i f i c a ç ã o   n a   Q u a r t a

Q -   E l a   r e c e b e   a   n o t i f i c a ç ã o   n a   Q u i n t a

S -   E l a   r e c e b e   a   n o t i f i c a ç ã o   n a   S e x t a  

As probabilidades são as descritas no enunciado

P A = 0,6

E a figura do enunciado demonstra várias probabilidades relacionadas ao fato de ser aceita ou não. Vamos calcular as seguintes probabilidades

a )   P ( M )

b )   P ( T | M C )

c )   P ( A | M c T c W c )

d )   P ( A | Q )

e )   P ( A | M c T c W c Q c F c )

Passo 2

A - O evento M pode ser dividido em duas partes, dependendo se ela é aceita (A) ou não:

P M = P M A + P M A c

Expandindo os termos, nós temos

P M = P M A P A + P M A c P A c

Substituindo os valores, nós obtemos o seguinte resultado

P M = 0,15 ∙ 0,6 + 0,05 ∙ 0,4 = 0,11

Passo 3

B – Vamos começar com a definição de probabilidade condicional, então

P T M c = P T ∩ M c P M c

Da letra a, podemos tirar a seguinte informação

P M c = 1 - P M → P M c = 0,89

Desde que T ⊆ M c , porque se o correio foi recebido na terça-feira, certamente não é recebido na segunda-feira:

T ∩ M c = T → P T ∩ M c = P ( T )

P ( T ) pode ser calculada do mesmo jeito que P ( M ) :

P T ∩ M c = P T

Expandindo os termos, nós temos que

P T ∩ M c = P T A P A + P T A c P A c

Substituindo os valores, nós obtemos o seguinte resultado

P T ∩ M c = 0,20 ∙ 0,6 + 0,10 ∙ 0,4 = 0,16

Substituindo os valores encontrados, temos a probabilidade condicional pedida na questão

P T M c = 0,16 0,89 ≈ 0,1798

Passo 4

C – Começando com a seguinte definição:

P A M c T c W c = P A ∩ M c T c W c P M c T c W c

Pelo princípio de DeMorgan, nós temos

P M c T c W c = P [ M ∪ T ∪ W c ]

Primeiro nós vamos usar antes a propriedade de probabilidade declarada, e então que M, T e W são eventos mutuamente exclusivos, com isso,

P M ∪ T ∪ W c = 1 - P M ∪ T ∪ W = 1 - [ P M + P T + P W ]

Vamos obter P ( W ) assim como obtemos P M e P ( T )

P W = P W A P A + P W A c P ( A c )

Substituindo os valores, nós temos que

P W = 0,25 ∙ 0,6 + 0,10 ∙ 0,4 = 0,19

Portanto,

P M ∪ T ∪ W c = 1 - 0,11 - 0,16 - 0,19 = 0,54

Para o nomeador da definição, vamos usar a seguinte identidade

P A ∩ M c T c W c = P M c T c W c A P ( A )

Vamos usar a identidade de Bayes e o fato de que a probabilidade condicional tem as mesmas propriedades de uma probabilidade simples

P M c T c W c A =   P [ M ∪ T ∪ W c | A ]

Com isso,

P M c T c W c A = 1 - P ( M ∪ T ∪ W | A )

Expandindo os termos, nós temos

P M c T c W c A = 1 - ( P M A + P T A + P W A )

Substituindo os valores conhecidos, nós obtemos

P M c T c W c A = 1 - 0,15 - 0,20 - 0,25 = 0,4

Portanto

P A M c T c W c = 0,4 ∙ 0,6 0,54 = 4 9  

Passo 5

D - Este é o uso direto do teorema de Bayes, com A e A c como hipóteses concorrentes

P A T = P T A P A P T A P A + P T A c P A c

Substituindo os valores citados, nós temos

P A T = 0,15 ∙ 0,6 0,15 ∙ 0,6 + 0,15 ∙ 0,4 = 0,6

Passo 6

E – Esta é calculada de forma análoga a letra c

P A M c T c W c Q c S c = P M c T c W c Q c S c P A P ( M c T c W c Q c S c )

Através da fórmula de Bayes e propriedades da probabilidade, temos que

P M c T c W c Q c S c | A = P [ M ∪ T ∪ W ∪ Q ∪ S C | A ]

Substituindo os valores, nós temos

P M c T c W c Q c S c | A = 1 - 0,15 - 0 - 0,20 - 0,25 - 0,15 - 0,10 = 0,15

Já temos todos os valores, podemos substituir

P A M c T c W c Q c S c = 0,15 ∙ 0,6 0,25 = 0,36

Resposta

a )   0,11

b ) ≈ 0,1798

c ) 4 9

d )   0,6

e ) 0,36

Exercícios de Livros Relacionados

A companhia de pizzas Dom utiliza testes de sabores e análise estatística de dados anteriores para comercializar novos produtos. Considere um estudo que envolva três tipos de crosta (fina, fina com al
De acordo com a revista Consumer Digest (julho/agosto, 1996), a provável localização de PCs (computadores pessoais) em uma residência é:Quarto do adulto: 0,03 Quarto da criança: 0,15 Outro quarto: 0,1
Há um interesse centrado na vida útil de um componente eletrônico. Suponha que se saiba que a probabilidade de que esse componente sobreviva mais que 6.000 horas é de 0,42. Suponha, também, que a prob
Uma indústria automobilística está preocupada com um possível recall de seu sedã quatro portas mais vendido. Se houver um recall, há 0,25 de probabilidade de que o defeito seja no sistema de freios; 0
Se cada item codificado em um catálogo começa com três letras distintas, seguidas de quatro dígitos distintos e diferentes de zero, determine a probabilidade de se selecionar, aleatoriamente, um desse