Nos exercícios 43 e 44, use os conjuntos de dados e os números de classes indicados para construir (a) uma distribuição de frequência expandida, (b) um histograma de frequência, (c) um polígono de frequência, (d) um histograma de frequência relativa e (e) uma ogiva.
Hospitais.
Número de classes: 8
Conjunto de dados: número de hospitais em cada estado. (Fonte: American Hospital Directory.)
12 100 52 73 354 52 34 8 212 116
13 40 17 142 99 61 76 114 81 50
22 109 56 88 72 16 103 11 28 14
75 37 28 203 156 103 36 176 12 65
27 116 377 35 89 7 62 75 39 13
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos lá, começando pela letra (a).
Bom para começarmos a trabalhar, temos que trazer aqui informações importantes que foram dadas no enunciado:
Número de classes: 8
Conjunto de dados: número de hospitais em cada estado. (Fonte: American Hospital Directory.)
12 100 52 73 354 52 34 8 212 116
13 40 17 142 99 61 76 114 81 50
22 109 56 88 72 16 103 11 28 14
75 37 28 203 156 103 36 176 12 65
27 116 377 35 89 7 62 75 39 13
Para começarmos, temos que determinar as 6 classes que foram informadas para a gente, ficando:
Beleza, além disso, precisamos determinar a frequência dessas classes. Lembrando que a frequência nesse caso vai ser o número de resultados que estão presentes nas faixas acima:
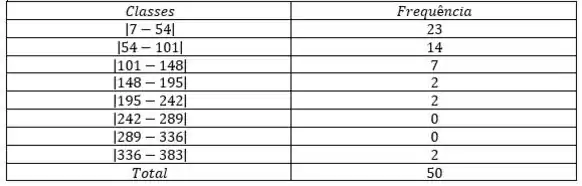
Com isso, podemos calcular tanto a frequência relativa quanto a acumulada.
Passo 2
Vamos calcular aqui.
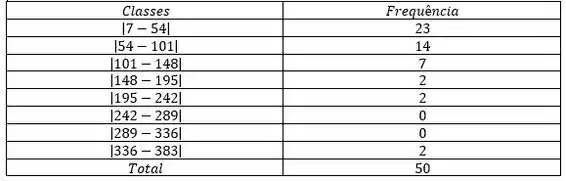
Para calcular a frequência relativa, vamos usar a fórmula:
Lembrando que é a frequência da classe. Além disso, importante lembrar que a frequência acumulada é a soma de todas as frequências até a classe calculada.
Calculando a frequência relativa e acumulada de cada classe, vamos ter:
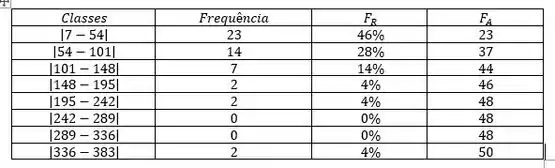
Show, com isso vamos conseguir montar o nosso histograma.
Passo 3
Vamos para a letra (b). Aqui vamos montar o nosso histograma:
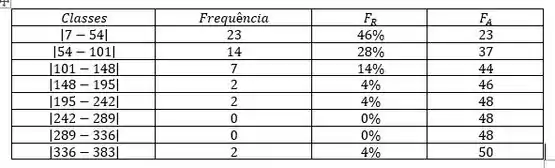
Nosso histograma vai ficar:
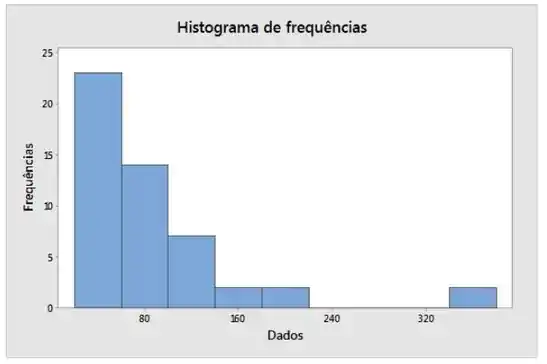
Passo 4
Agora para a letra (c). Aqui, vamos montar o polígono de frequência:
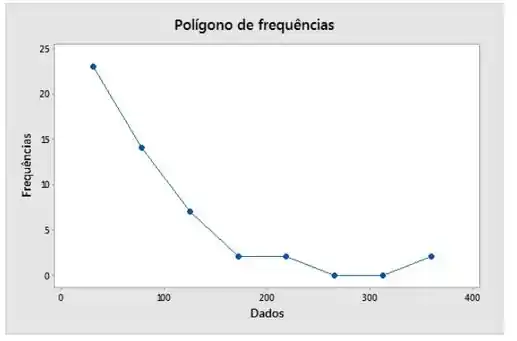
Passo 5
Agora para a letra (d). Aqui, vamos montar o histograma da frequência relativa:
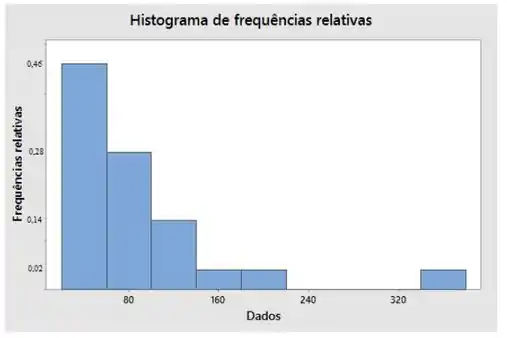
Passo 6
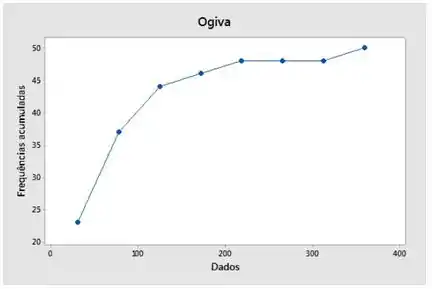
Agora para a letra (e). Aqui, vamos montar o gráfico ogiva: