Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 8.Exercícios propostos - Ex. 12

Um fabricante faz a remessa de 1.000 lotes, de 100 parafusos cada um. Se 5% dos parafusos são normalmente defeituosos, em quantos lotes pode-se esperar que existam:

  1. menos que 90 parafusos perfeitos;
  2. 98 ou mais parafusos perfeitos.

Passo 1

Oi pessoal. Vamos pensar juntos neste exercício?!

Pelo enunciado temos os seguintes dados:

  • n = 10 0 ;
  • p = 0 , 95 ;
  • q = 0 , 05 .

Onde:

μ = n ∙ p = 10 0 ∙ 0 , 95 = 95

σ = n ∙ p ∙ q = 10 0 ∙ 0 , 95 ∙ 0 , 05 = 2,1 8

No item a) queremos saber em quantos lotes pode-se esperar que existam menos de 90 parafusos perfeitos:

P x < 90

Então iremos calcular z para x = 90 - 0,5 = 89,5 :

z = x - μ σ = 8 9,5 - 95 2,1 8 = - 2,52

Pela Tabela da Distribuição normal, temos:

P x < 89 , 5 = 0 , 0059

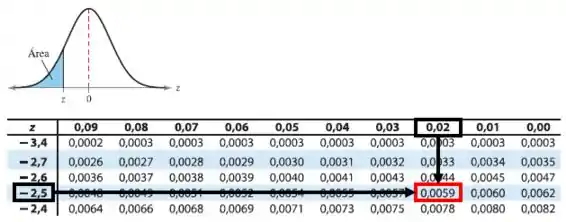
Para menos que 90 parafusos perfeitos, podemos esperar que existam:

0 , 0059 ∙ 100 0 ≈ 6   l o t e s

Passo 2

No item b) queremos saber em quantos lotes pode-se esperar que existam 98 ou mais parafusos perfeitos. Para 98 parafusos perfeitos temos o seguinte:

P x ≥ 98 = P 97,5 < x < 98,5 + [ 1 - P x < 98,5 ]

Para x = 97 , 5 :

z 9 7 , 5 = 9 7 , 5 - 95 2,1 8 = 1,1 5

E para x = 98 , 5

z 98 , 5 = 98 , 5 - 12 2,1 8 = 1 , 6 1

Pela Tabela da Distribuição normal, temos:

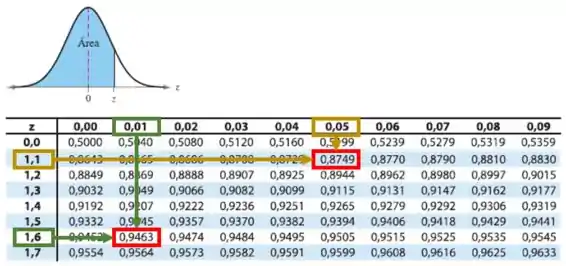
Pela tabela, temos:

  • P x < 97,5 = 0,8749 ;
  • P x < 98,5 = 0,9463 .

Então temos o seguinte:

P x ≥ 98 = P 97,5 < x < 98,5 + [ 1 - P x < 98,5 ]

P x ≥ 98 = 0,9463 - 0,8749 + 1 - 0,9463 = 0,1251

Para 98 ou mais parafusos perfeitos, podemos esperar que existam:

0 , 1251 ∙ 1000 ≈ 125   l o t e s

Tchau galerinha! Te espero em mais exercícios.

Resposta

  1. 6 lotes;
  2. 125 lotes.

Exercícios de Livros Relacionados

Para uma distribuição de qui-quadrado com 12 graus de liberdade, determinar o valor de X c 2 de modo que:a área à direita desse ponto seja de 5%;a área à esquerda desse ponto seja de 99%.
Determinar os valores de t 1 , para a distribuição de Student, que satisfaçam cada uma das seguintes condições:área entre - t 1 e t 1 de 90%, com ϕ = 25 ;área à esquerda de - t 1 de 2,5%, com ϕ = 20 ;
Se a variável X apresenta uma distribuição de Student com ϕ = 10 , determinar a constante K de modo que:
Certas válvulas produzidas por uma empresa têm vida média de 900 h e desvio padrão de 80 h. A empresa envia 1.000 lotes, de 100 válvulas cada um. Em quantos lotes pode-se esperar que:a vida média exce