Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 6.1 - Ex. 4c
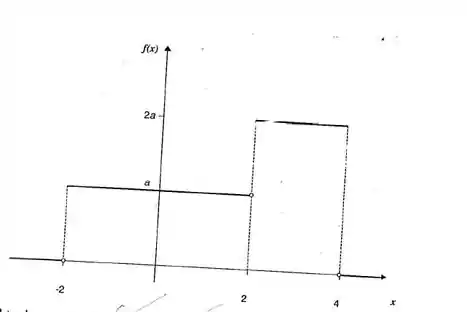
O gráfico abaixo representa a densidade de uma variável aleatória
c. Calcule
Passo 1
Eai,tudo bem? Bora resolver mais um exercício?
O exercício nos pede para calcular o valor de com base na função densidade de probabilidade dada. Certo?
Pois bem, você se lembra desse conceito? Porque se não, é hora de dar aquela revisão!
Passo 2
Calculando o valor esperado de temos:
Passo 3
Observando o gráfico, chegamos a conclusão de pois .
Agora vamos calcular porque precisaremos para o cálculo da variância. Ok?
Passo 4
Logo, a variância de será dada por:
Resposta
Assim, concluímos o exercício
Exercícios de Livros Relacionados
Após embaralhar um baralho de 52 cartas, um crupiê dá cinco cartas. Seja X = número de naipes representados na mão de cinco cartas.Mostre que a fmp de X éCalcule μ ,σ 2 eσ
De todos os clientes que compram portões automáticos de garagem, 75% compram um modelo acionado por corrente. Seja X = número entre os próximos 15 compradores que selecionam o modelo acionado por corr
98. Quando as placas de circuito usadas na fabricação de CD-players são testadas, a porcentagem de peças com defeito no longo prazo é 5%. Suponha que um lote de 250 placas tenha sido recebido e que a
95. O tempo de conclusão X de uma determinada tarefa possui fdc F(x) dada por 0 x0 x 3 3 0 ≤ x1 1 - 1 2 7 3 - x 7 4 - 3 4 x 1 ≤ x7 3 1 x ≥ 7 3 a. Obtenha a fdp f(x).b. Calcule P(0,5 ≤ X ≤ 2). c. Calcu
96. A tensão de ruptura de um determinado tipo de diodo escolhido aleatoriamente possui distribuição normal com valor de média 40 V e desvio padrão 1,5 V. a. Qual é a probabilidade de a voltagem de um