Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 6.3 - Ex. 5a
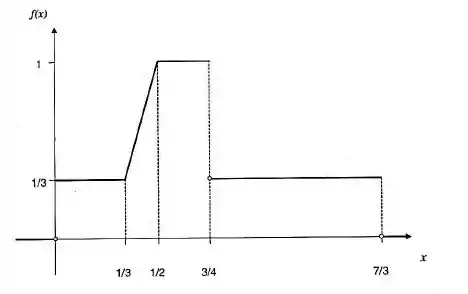
O gráfico a seguir representa a densidade de uma variável aleatória contínua
- Verifique que representa uma função de densidade.
Passo 1
Eai,tudo bem? Bora resolver mais um exercício?
O exercício nos pede para verificar que representa uma função de densidade.
Você se lembra desse conteúdo? Se não, é hora de dar aquela revisão. Ok?
Passo 2
Calculando a área do gráfico de temos que:
Resposta
E assim, verificamos o que representa uma função de densidade
Exercícios de Livros Relacionados
O artigo “Modeling Sediment and Water Column Interactions for Hydrophobic Pollutants” (Water Research, 1984, p. 1169-1174) sugere a distribuição uniforme no intervalo (7,5, 20) como modelo para a prof
A fdc da duração da retirada X descrita no Exercício 1 é f x = 0x- 2 1 2 + 3 32 4 x - x 3 3 - 2 ≤ x2 1 2 ≤ x Use tais condições para calcular os itens a seguira. Calcule P ( X0 ) .b. Calcule P ( - 1X1
A fdc da duração da retirada X descrita no Exercício 1 é f x = 0x0 x 2 4 0 ≤ x2 1 2 ≤ x Use tais condições para calcular os itens a seguira. P ( X ≤ 1 ) b. P ( 0,5 ≤ X ≤ 1 ) c. P ( X0,5 ) d. A mediana
O Exemplo 4.4 apresentou o conceito de tempo de avanço no fluxo de tráfego e propôs uma distribuição particular para X o tempo de avanço entre dois carros consecutivos selecionados aleatoriamente (em
Uma pessoa deve chegar ao escritório onde trabalha até as 9 horas. Devido ao tráfego e a fatores outros ele chega atualmente entre 8 : 45 e 9 : 05 horas. A frequência relativa de suas diversas chegada