Um grande lote de componentes chegou em um distribuidor e só pode ser classificado como aceitável se a proporção de componentes com defeito for no máximo 0,10. O distribuidor decide selecionar 10 componentes aleatoriamente e aceitar o lote apenas se o número de componentes defeituosos da amostra for no máximo 2.
a. Qual é a probabilidade de o lote ser aceito quando a proporção real de itens com defeito for 0,01? 0,05? 0,10? 0,20? 0,25?
b. Seja p a proporção real de itens com defeito no lote. Um gráfico de P(lote é aceito) em função de p, com p no eixo horizontal e P(lote é aceito) no eixo vertical é denominado curva característica de operação do plano de aceitação da amostragem. Use os resultados da parte (a) para fazer o gráfico da curva para .
c. Repita as partes (a) e (b) com “1” substituindo “2” no plano de aceitação da amostragem.
d. Repita as partes (a) e (b) com “15” substituindo “10” no plano de aceitação da amostragem. e. Qual dos três planos de amostragem é mais satisfatório e por quê?
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Denote com pp a proporção (real) de componentes defeituosos. E deixar
No nosso caso, n=10n=10 e pp é a proporção real, o que significa que X pode distribuição binomial
Passo 2
- Dependendo dos valores de pp, a probabilidade de aceitação será diferente. Denotar evento
- Como mencionamos, P(A) é uma função de p
- Substituindo "2" por "1", temos o seguinte:
- Da mesma forma que acima, substitua 10 por 15, temos:
- No exercício, podemos ver quando o lote é aceitável (quando pp é no máximo 0,1), é por isso que olhamos as figuras para ver quando P(A) é alto para p≤0,1 (e baixo para p>0.1). Podemos ver que o plano da parte (d) talvez seja o melhor, então escolheríamos esse plano. É o mais satisfatório.
Nos é dado que o lote será aceito se no máximo 2 de 10 forem defeituosos, portanto, a fórmula geral para pp seria
Função de densidade cumulativa cdf da variável aleatória binomial X com parâmetros n e p é
Para diferentes pp, obteremos resultados diferentes. Podemos concluir que P(A) é na verdade uma função de p.
Para , o seguinte é verdade
Para , o seguinte é verdade
Para , o seguinte é verdade
Para , o seguinte é verdade
Para , o seguinte é verdade
A curva característica de operação exata é fornecida abaixo.
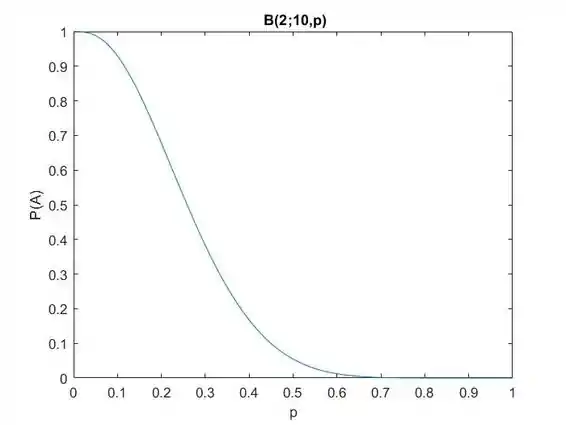
Para , o seguinte é verdade
Para , o seguinte é verdade
Para , o seguinte é verdade
Para , o seguinte é verdade
Para , o seguinte é verdade
E a figura a seguir é curva característica operacional para este caso.
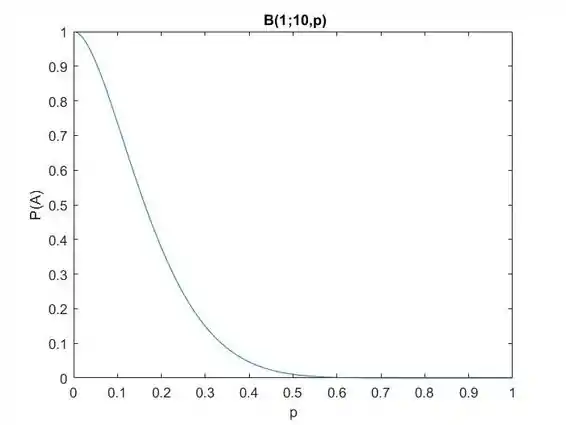
Passo 3
Para p=0.01, o seguinte é verdadeiro
Para , o seguinte é verdade
Para , o seguinte é verdade
Para , o seguinte é verdade
Para , o seguinte é verdade
Para , o seguinte é verdade
E a figura a seguir é curva característica operacional para este caso.
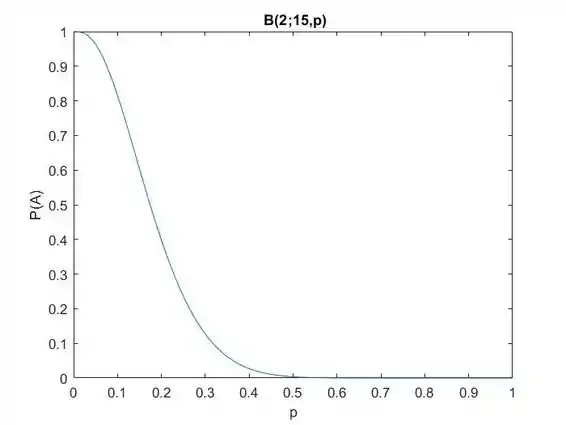
Alguém pode escolher o plano para a parte (a) também, mas certamente parece que a parte (d) é a melhor das três dadas
Resposta
- Ver o desenvolvimento
- Plano da parte d