Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 4.1 - Ex. 28

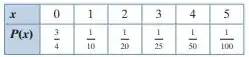
Identificando distribuições de probabilidade. Nos exercícios 27 e 28, determine se a distribuição é uma distribuição de probabilidade. Se não for, explique o porquê.

Passo 1

Fala galera boa, tudo bem? Vamos para mais uma questão de distribuição de probabilidades. A tabela de distribuição de probabilidades dada no exercício 28, mostrada no enunciado, deve ter a soma de todas as probabilidades igual a 1 e não ter nenhuma probabilidade negativa. Então, como vocês sabem:

P 0 + P 1 + P 2 + P 3 + P 4 + P 5 = 1

Passo 2

Deste modo, basta substituir os valores das probabilidades como é feito abaixo:

3 4 + 1 10 + 1 2 0 + 1 25 + 1 5 0 + 1 10 0 = 1

Passo 3

Para facilitar as contas, vamos resolver as frações:

0,75 + 0,10 + 0,05 + 0,04 + 0,02 + 0,01 = 1

0,97 ≠ 1

Opa, a soma das probabilidades não é igual a 1. Desse modo, a tabela dada na questão 28 não pode ser considerada como uma distribuição de probabilidades, pois não satisfaz as condições necessárias para tal.

É isso aí galerinha, até a próxima.

Resposta

A tabela não é uma distribuição de probabilidades, pois o somatório das probabilidades é menor que 1.

Exercícios de Livros Relacionados

Sejam E 1 ,E 2eE 3 as amostras que obedecem à especificação de percentual de sólidos, à especificação de peso molecular e à especificação de cor, respectivamente. Um total de 240 amostras é classifica
Um lote de 50 arruelas contém 30 delas que são mais espessas do que a dimensão desejada. Suponha que três arruelas sejam selecionadas ao acaso, sem reposição no lote.Qual é a probabilidade de todas as
Computadores, em um carregamento de 100 unidades, contêm um HD portátil e um leitor/gravador de CD ou ambos, de acordo com a tabela seguinte:Seja A o evento em que um computador possui o HD portátil e
Dois fabricantes, forneceram cada um, 2.000 peças, que foram avaliadas com relação ao atendimento de especificações . Um tipo de peça era de maior complexidade que outra. A proporção de peças não conf
O circuito a seguir opera se, e somente se, houver um caminho de dispositivos funcionais, da esquerda para a direita. Considere que dispositivos falhem independentemente, sendo a probabilidade de falh