Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 9.Exercícios - Ex. 40

Dois tipos de iscas de peixe, uma feita de tubos de argila vitrificada e outra de blocos de concreto e escova, foram usados durante 16 períodos de tempo diferentes durante 4 anos no lago Tohopekaliga, Flórida ("Two Types of Fish Attractors Compared in Lake Tohopekaliga, Florida", Trans. Amer. Fisheries Soc., 1978, p. 689-695). As observações a seguir referem-se a peixes pescados por dia de pescaria:

Na média, uma isca parece ser mais eficaz que a outra? a. Use o teste t pareado com 0,01 para testar H0: D 0 versus Ha: D 0. b. O que acontece se o teste t de duas amostras for usado (s1 2,48 e s2 2,91)?

Passo 1

  1. Dado

    2. α = 0.05

    Determine a diferença de valor de cada par.

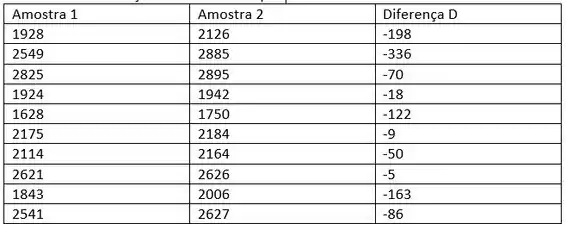
    Passo 2

    Dada a alegação: a diferença entre P e L é maior que 25.

    A afirmação é a hipótese nula ou a hipótese alternativa. A hipótese nula e a hipótese alternativa afirmam o oposto uma da outra. A hipótese nula precisa conter o valor mencionado na reivindicação.

    H 0   :   μ d =   - 25

    H a   ;   μ d <   - 25

    Determine a média amostral das diferenças. A média é a soma de todos os valores dividido pelo número de valores

    d - = - 198 - 336 - 70 + … - 5 - 163 - 86 10   ≈   - 105.7

    Determine o desvio padrão da amostra das diferenças:

    s d = - 198 - 105 . 2 + … + 86 - - 105.7 2 10 - 1   ≈ 103.8450

    Determine o valor da estatística de teste:

    t = d - - d s d n = - 105.7 - - 25 103.8450 10 ≈ 2.457

    O valor P é a probabilidade de obter o valor da estatística de teste, ou um valor mais extremo, assumindo que a hipótese nula é verdadeira. O valor P é o número (ou intervalo) no título da coluna da distribuição T de Student no apêndice contendo o valor t na linha d f = n - 1 = 10 - 1 = 9

    0.01 < P < 0.025

    Se o valor P for menor que o nível de significância, rejeite a hipótese nula.

    P < 0.05   → R e j e i t a r   H 0

    Há evidências suficientes para apoiar a alegação de que o conteúdo mineral ósseo total médio real do corpo durante o pós-desmame excede aquele durante a lactação em mais de 25 g.

    Passo 3

  2. c = 95 = 0.95

    3. Determine o t α 2 usando a tabela de distribuição de Student's T no apêndice com d f = n - 1 = 10 - 1 = 9 :

    t 0.05 = 1.833

    A margem de erro é então:

    E = t α 2 ∙ s d n = 1.833 ∙ 103.8450 10   ≈ - 45.5067

    Assim, o limite de confiança superior é - 45.5067 .

  3. A média é a soma de todos os valores dividido pelo número de valores:

x 1 - = 1928 + 2549 + 2825 + … + 2621 + 1843 + 2541 10 = 2214.8

x 2 - = 2126 + 2885 + 2895 + … + 2626 + 2006 + 2627 10 = 2320.5

A variância é a soma dos desvios quadrados da média dividida por n-1n−1. O desvio padrão é a raiz quadrada da variância:

s 1 =   1928 - 2214.8 2 + … + 2541 - 2214.8 2 10 - 1 ≈ 396.7327

s 2 = 2126 - 2320.5 2 + … + 2627 - 2320.5 2 10 - 1 ≈ 406.1445

Determine a estatística de teste:

t = x 1 - - x 2 - - μ 1 - μ 2 s 1 2 n 1 + s 2 2 n 2 = 2214.8 - 2320.5 - 25 396.7327 2 10 + 406.1445 2 10 ≈ - 0.449

Determine os graus de liberdade (arredondados para o inteiro mais próximo):

∆   = s 1 2 n 1 + s 2 2 n 2 2 s 1 2 n 1 2 n 1 - 1 + s 2 2 n 2 2 n 2 - 1 = 396.7327 2 10 + 406.1445 2 10 2 396.7327 2 10 2 10 - 1 + 406.1445 2 10 2 10 - 1 ≈ 17

O valor P é a probabilidade de obter o valor da estatística de teste, ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da distribuição T de Student no apêndice contendo o valor t na linha df=17:

P > 0.10

Se o valor P for menor ou igual ao nível de significância, então a hipótese nula é rejeitada:

P > 0.05 ⇒   F a l h a   a o   r e j e i t a r   H 0

Observamos então que chegamos a uma conclusão diferente em comparação com a parte (a).

Resposta

  1. Há evidências suficientes para apoiar a alegação de que o conteúdo mineral ósseo total médio real durante o pós-desmame excede aquele durante a lactação em mais de 25 g.

  2. -45.5067

  3. Não é a mesma conclusão

Exercícios de Livros Relacionados

Determine a quantidade de graus de liberdade para o teste t de duas amostras ou IC em cada uma das situações a seguir:a. m = 10 , n = 10 , s 1 = 5,0 , s 2 = 6,0 b. m = 10 , n = 15 , s 1 = 5,0 , s 2 =
Para decidir se dois tipos diferentes de aço possuem os mesmos valores de dureza de fratura média real, n espécimes de cada tipo são testados, produzindo os seguintes resultados:Calcule o valor P para
a. Mostre para o teste de cauda superior c o m ⁡ σ 1 e σ 2 conhecidos que, à medida que m ou n aumenta, β diminui quando μ 1 - μ 2Δ 0 .b. Para o caso de tamanhos das amostras iguais ( m = n) e α fixo,
Sejam μ 1 e μ 2 as vidas médias reais de duas marcas concorrentes de pneus radiais de tamanho P205/65R15. Teste H 0 : μ 1 - μ 2 = 0 versus H u : μ 1 - μ 2 ≠ 0 no nível 0,05 , usando os seguintes dados
As pessoas que têm a síndrome de Reynaud estão propensas a sofrer uma diminuição repentina da circulação sangüínea nos dedos dos pés e das mãos. Em um experimento para estudar a extensão dessa deficiê