Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 3.Exercícios - Ex. 11

Uma instalação de recondicionamento de automóveis especializada em regulagem de motores sabe que 45% de todas as regulagens são feitas em automóveis de quatro cilindros, 40% em automóveis de seis cilindros e 15% em automóveis de oito cilindros. Seja X número de cilindros do próximo carro a ser preparado.

a. Qual é a fmp de X?

b. Desenhe um gráfico de linhas e um histograma de probabilidade da fmp da parte (a).

c. Qual é a probabilidade de o próximo carro a ser regulado ter no mínimo seis cilindros? Mais de seis cilindros?

Passo 1

  1. Considere a variável aleatória XX definida no exercício. Por ser uma variável aleatória discreta, ela possui uma função de massa de probabilidade.

    Comentário. A Função de Massa de Probabilidade (pmf) de uma variável aleatória discreta XX é dada por

    p x = P   X = x = P ω   ϵ   S   : X ω   = x

    para cada número x.

    As probabilidades são dadas no exercício como porcentagens, ou seja, por exemplo, ( X = 4 ) = 40 % = 0 . 45 . Portanto, a função massa de probabilidade é dada por

    P X = 4   = 0.45

    P   X = 6 = 0.4

    P   X = 8 = 0.15

    E P X = x = 0 para todos os outros x.

    Passo 2

    3. Passo 3

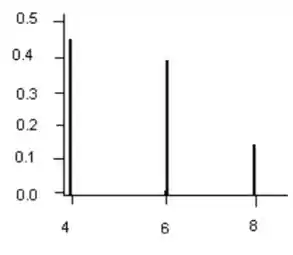
  3. Para o caso de pelo menos seis, é verdade que

P X   ≥ 6   = P X =   6 + P X = 8   = 0.4 + 0.15 = 0.55

Para o caso de o carro ter mais de seis cilindros, é verdade que o carro pode ter apenas 8 cilindros. Assim, vale o seguinte

P X > 6 = P X = 8 = 0.15

Resposta

  1. P X = 4 = 0.45 ,   P X = 6 = 0.4 ,   P X = 8 = 0.15
  2. P   X   ≥ 6 = 0.55 ,   P X > 6 = 0.15

Exercícios de Livros Relacionados

Para evitar a detenção na alfândega, um viajante coloca seis tabletes de narcóticos em um frasco com nove pílulas de vitamina, que são similares em aparência. Se o fiscal da alfândega selecionar três
Um fabricante sabe que, na média, 20 % das torradeiras elétricas que ele produz necessitarão de reparos dentro de um ano após serem vendidas. Ao selecionar 20 torradeiras aleatoriamente, encontre os n
Se sete cartas são retiradas de um baralho comum com 52 cartas, qual é a probabilidade de que(a) exatamente duas delas sejam cartas com figuras?(b) pelo menos uma carta seja uma dama?
Suponha que, para um grande carregamento de chips de circuito integrado, a probabilidade de falha em qualquer um deles seja de 0,10. Assumindo que as suposições que fundamentam as distribuições binomi
Vinte por cento de todos os telefones de um determinado tipo são enviados para reparo em garantia. Desses, 60% podem ser reparados, enquanto os outros 40% devem ser substituídos. Se uma empresa compra