Um importante sistema age como apoio para um veículo do programa espacial. Um componente único e crucial opera somente 85% do tempo. Para aumentar a confiabilidade no sistema, decidiu-se que três componentes serão instalados em paralelo, de modo que o sistema falhe somente se todos os componentes falharem. Assuma que os componentes funcionem independentemente e que sejam equivalentes no sentido de que todos têm 85% de taxa de sucesso. Considere a variável aleatória o número de componentes, dentre os três,
que falham.
(a) Escreva a função de probabilidade para a variável aleatória .
(b) Qual é (ou seja, o número médio de componentes, dentre os três, que falham)?
(c) Qual é a ?
(d) Qual é a probabilidade de que o sistema inteiro tenha sucesso?
(e) Qual é a probabilidade de que o sistema falhe?
(f) Se desejarmos ter um sistema com 0,99 de probabilidade de sucesso, os três componentes são suficientes? Se não, quantos são necessários?
Passo 1
Falaa, meu querido/minha querida. A variável aleatória tem distribuição binomial, e a sua função de densidade cumulativa é dada por:
Então, bora para os cálculos!!!
Passo 2
Vamos considerar sucesso o tempo e que o componente não opera, logo, a probabilidade de sucesso é . Sendo assim, o insucesso é dado por .
Como nós temos 3 componentes que falham .
Portanto, a função massa de probabilidade é:
Enquanto, a distribuição de probabilidade da variável é:
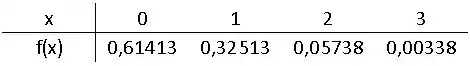
Passo 3
Para uma variável aleatória binomial com parâmetros , e , o valor esperado é dado pela fórmula abaixo:
Passo 4
Já a variância é descrita da seguinte forma:
Passo 5
Agora, precisamos encontrar a probabilidade de que o sistema continue, o evento que descreve essa situação é que 2 ou menos componentes falhem.
Passo 6
Para o sistema não funcionar, quer dizer que os 3 componentes falharam, e essa probabilidade é dada por:
Passo 7
Como a probabilidade na letra (d) é quase 1, podemos concluir que 3 componentes são suficientes.
Resposta
Resolução nos passos anteriores.