Uma moeda é lançada até que uma cara ocorra e, então, o número X de lançamentos é registrado. Depois de repetirmos o experimento 256 vezes, obtemos os seguintes resultados:

Teste a hipótese no nível de significância de 0,05 de que a distribuição observada de X pode ser ajustada pela distribuição geométrica
Passo 1
E ai seres de luz, tudo bem?
Como diz o Homer “Filho, este aparelhinho vai nos ajudar a escapar dessa fria!”

O objetivo do estudo é testar e determinar se a distribuição observada de X pode ser ajustada pela distribuição geométrica
As hipóteses nulas e alternativa são,
Os graus de liberdade são,
Seja o nível de significância
Valor crítico:
Usando as tabelas de distribuição, ao nível de 5% para 7 graus de liberdade, o valor crítico é
14,07.
Região de rejeição:
Se então a hipótese nula deve ser rejeitada.
Sob a hipótese nula, a fórmula para a estatística do teste qui-quadrado é
Passo 2
A função de massa de probabilidade da distribuição geométrica com parâmetro é de
Vamos considerar a tabela a seguir

Passo 3
Uma vez que as frequências observadas são inferiores a 5, estão sendo adicionadas à frequência acima. Depois de agrupar as últimas três linhas da tabela acima, conforme mostrado abaixo:
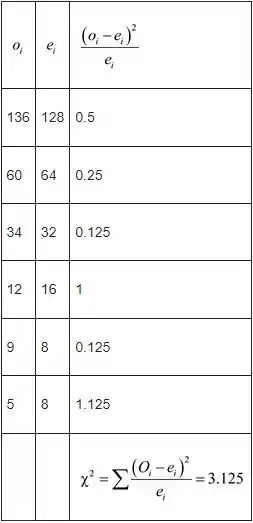
A partir da tabela acima, as estatísticas são
Aqui, pode-se observar que o valor calculado (3,125) é menor que o valor crítico (14,07).
Portanto, a hipótese nula não pode ser rejeitada.
Portanto, pode-se concluir que a distribuição observada pode ser ajustada pela distribuição
Geométrica
“Eu não estava mentindo! Estava escrevendo ficção com a boca.”

Resposta
Resposta nos passos