Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 5.Exercícios - Ex. 5

O número de clientes esperando no serviço de embalagens para presente em uma loja é uma va X com valores possíveis 0, 1, 2, 3, 4 e probabilidades correspondentes 0,1, 0,2, 0,3, 0,25, 0,15. Um cliente selecionado aleatoriamente terá 1, 2 ou 3 pacotes para embrulhar com probabilidades 0,6, 0,3 e 0,1, respectivamente. Seja Y = o número total de pacotes a serem embrulhados para os clientes que estão na fila (assuma que o número de pacotes de um cliente seja independente do número de pacotes de qualquer outro cliente).

a. Determine P ( X = 3 ,   Y = 3 ) , isto é, p ( 3 ,   3 ) .

b. Determine p ( 4 ,   11 ) .

Passo 1

Falaaa, meu querido/minha querida. Como vai?? Nós podemos extrair a seguinte tabela do enunciado para a variável aleatória X .

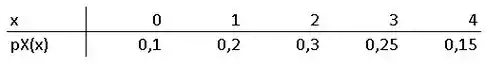
Essa variável modela o numero de clientes esperando. Bora lá finalizar a questão!!!

Passo 2

A primeira probabilidade é P ( X = 3 ,   Y = 3 ) , vamos montando a equação.

P X = 3 , Y = 3 = P ( 3   c l i e n t e   a   e s p e r a ,   3   p a c o t e s   p a r a   e m b r u l h a r )

= P ( 3   c l i e n t e s   e s p e r a n d o ,   1   p a c o t e   c a d a )

= P 1   p a c o t e   c a d a     3   c l i e n t e s   e s p e r a n d o ) ∙ P ( 3   c l i e n t e s   e s p e r a n d o )

= 0,6 ∙ 0,6 ∙ 0,6 ∙ 0,25

p ( 3 ,   3 ) = 0,054

Passo 3

Seguindo a mesma lógica da letra (a)

p 4 ,   11 = P ( 4   c l i e n t e s   e s p e r a n d o ,   11   p a c o t e s   p a r a   e m b r u l h a r )

= P 11   p a c o t e s   p a r a   e m b r u l h a r     4   c l i e n t e s   e s p e r a n d o ) ∙ P ( 3   c l i e n t e s   e s p e r a n d o )

= 4 ∙ 0,1 3 ∙ 0,3 ∙ 0,15

p ( 4,11 ) = 0,00018

Resposta

  1. p ( 3 ,   3 ) = 0,054

  2. p 4 ,   11 = 0,00018

Exercícios de Livros Relacionados

As informações da tabela a seguir foram coletadas de 24 pacientes da área de cardiologia de um grande hospital público. A variável C indica o número de intervenções cirúrgicas sofridas pelo paciente,
Para o lançamento de dois dados equilibrados, defina duas variáveis aleatórias. Seja X o número de vezes que aparece a face 2 e Y igual a 0 se a soma for par e 1, caso contrário.Determine a função de
O departamento de vendas de certa companhia ofereceu um curso de atualização a seus funcionários e, para estudar a eficácia do curso, resolveu comparar a noto de teste no curso (7) com o volume de ven
Duas moedas são lançadas simultaneamente. Uma delas é equilibrada e a outra tem probabilidade 2 / 3 de sair face cara. Considere as variáveis U : total de caras observadas e V é uma Bernoulli que assu
Determine o valor de c que faz a função ser uma função de probabilidades conjuntas em nove pontos com x = 1,2,3 e y = 1, 2,3. Determine o seguinte: P ( X = 1 ,Y4 ) P ( X = 1 ) P ( Y = 2 ) P ( X2 ,Y2 )