Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 11.Problemas - Ex. 1
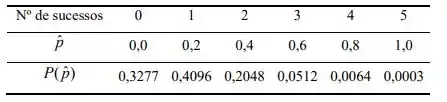
Obtenha a distribuição de quando . Depois calcule .
Passo 1
Primeiro, vamos obter a distribuição de quando e .
Conside que representa o número de sucessos na nossa amostra de tamanho 5.
Sabemos que tem distribuição binomial com parâmetros n e p, logo usando a função de probabilidade da distribuição binomial, temos
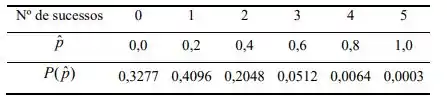
Passo 2
Agora, falta calcularmos .
O estimador teve sua distribuição amostral estudada na seção 10.9. De lá podemos concluir que tem distribuição aproximadamente normal, com parâmetros:
Trazendo para o nosso problema, temos
Resposta
Exercícios de Livros Relacionados
Considere uma amostra aleatória X 1 , … , X n da fdp f ( x ; θ ) = 0,5 ( 1 + θ x ) - 1 ≤ x ≤ 1 em que - 1 ≤ θ ≤ 1 (essa distribuição surge na física de partículas). Mostre que θ ˆ = 3 X ‾ é um estimad
Os dados que seguem sobre a resistência à flexão (MPa) das vigas de um tipo de concreto foram introduzidos no Exemplo 1.2 5,97,27,36,38,16,87,07,66,86,57,06,37,99,08,28,77,89,77,47,79,77,87,711,611,31
Usando um bastão longo de comprimento μ , você traçará um gráfico quadrado em que o comprimento de cada lado é μ . Assim, a área do gráfico será μ 2 . Entretanto, você não conhece o valor de μ , então
De n 1 fumantes do sexo masculino escolhidos aleatoriamente, X 1 fumavam cigarro com filtro, enquanto de n 2 fumantes do sexo feminino selecionadas aleatoriamente, X 2 fumavam cigarro com filtro. Repr
Seja X uma distribuição de Weibull com parâmetros α e β , então E ( X ) = β ⋅ Γ ( 1 + 1 / α ) V ( X ) = β 2 Γ ( 1 + 2 / α ) - [ Γ ( 1 + 1 / α ) ] 2 a. Com base em uma amostra aleatória X 1 , … , X n ,