Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 11.Problemas - Ex. 2
Encontre um limite superior para quando . Faça o gráfico em cada caso.
Passo 1
Primeiro, vamos encontrar um limite superior para quando .
Considere
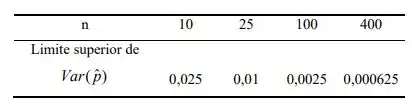
Montando uma tabelinha com os valores dos limites superiores, temos
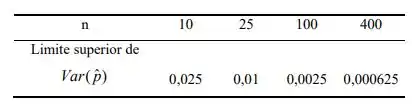
Passo 2
Construindo o gráfico, fica mais ou menos assim...
Resposta
Exercícios de Livros Relacionados
Uma amostra de n aeronaves Pandemonium jet fighters capturadas resulta em números de série x 1 , x 2 , x 3 , … , x n . A CIA sabe que cada aeronave foi numerada consecutivamente na fábrica, começando
O artigo do qual os dados do Exercício 1 foram tirados também forneceu as observações de resistência a seguir para os cilindros 6,15,87,87,17,29,26,68,37,08,37,88,17,48,58,99,89,714,112,611,2 Antes de
Uma amostra aleatória de n capacetes de ciclista fabricados por uma empresa é selecionada. Seja X = número entre os n que esteja com defeito, e p = P (com defeito). Assuma que somente X seja observado
Suponha que o crescimento médio real μ de um tipo de planta durante o período de um ano seja idêntico ao de um segundo tipo, mas a variância de crescimento do primeiro tipo seja σ 2 , enquanto a do se
Seja X 1 , X 2 , … , X n uma amostra aleatória de uma distribuição de Rayleigh com fdp f ( x ; θ ) = x θ e - x 2 ( 2 θ )x0 a. Pode-se mostrar que E X 2 = 2 θ . Use esse fato para construir um estimado