Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 11.Problemas - Ex. 22b
Um pesquisador está em dúvida sobre duas possíveis estatísticas, t e t’, para serem usadas como estimadores de um parâmetro θ. Assim, ele decidiu usar simulação para uma situação hipotética, procurando encontrar pistas que o ajudassem a decidir qual o melhor estimador. Partindo de uma população fictícia, onde θ = 10, ele retirou 1.000 amostras de 20 elementos, e para cada amostra calculou o valor das estatísticas t e t’. Em seguida, construiu a distribuição de freqüências, segundo o quadro abaixo.
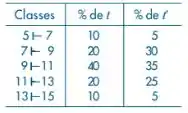
Verifique as propriedades de t e t’ como estimadores de θ. Qual dos dois você adotaria? Por quê?
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para acharmos as propriedades para o estimador. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser lembrar que, quando ele fala em propriedades, ele está falando da média, vício, variância e EQM. Então, vamos montar uma tabela com os valores vindos desses estimadores.
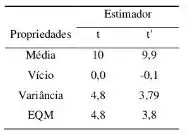
Passo 3
Com essa tabela, conseguimos ver que t é não-viesado, apesar de ter uma variância maior do que t’. Por isso, escolheria o t’.
Resposta
escolheria o t’.