Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 8.6 - Ex. 30
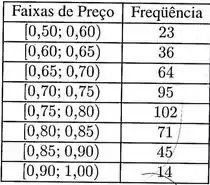
O preço unitário de mudas de laranjeira (em reais), em atacadistas especializados, é uma variável aleatória que se pretende modelar pela normal. Com base nos dados apresentados na tabela a seguir, teste a hipótese de que o modelo normal é adequado a esse caso, considerando um nível de significância de .
Passo 1
Oi deus, sou eu denovo!
Bora para mais um teste de aderência, dessa vez para a variável:
E deveremos realizar o seguinte teste:
Sempre bom relembrar, que realizamos o teste aproximando por uma distribuição , da seguinte forma:
Onde representa a quantidade de inteervalos, no nosso caso intervalos. E é a frequência observada em cada intervalo.
Já o é a frequência ESPERADA para cada intervalo se essa variável realmente tivesse a distribuição sugerida; ou seja, temos de encontrar esse valor.
Antes de sair calculado as frequências esperadas note que precisamos dos parâmetros , que não foram dados pelo enunciado; o que é um baita de um vacilo porque vamos ter que calcular isso com base na tabela dada.
Passo 2
Não sei se você lembra como fazemos isso, basicamente teremos que encontrar o ponto médio de cada intervalo para usar como o “representante” daquele intervalo, então vamos começar fazendo isso; para facilitar fiz outra tabela já com os pontos médios de cada intervalo:
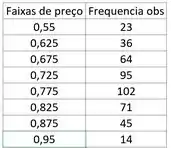
Cabe lembrar, caso tenha esquecido, que para obter o ponto médio de cada intervalo basta pegar os dois valores, somar e dividir por 2.
Então agora, vamos atrás da média e da variância:
E
Orra bicho! Cansamo já! Mas só agora podemos calcular a frequência esperada:
Lembrando que, temos de usar a aproximação pela normal PADRÃO, que possui a seguinte forma:
Portanto, fazendo essa substituição na probabilidade:
E
Agora basta olhar na tabela de distribuição normal, lembrando sempre que ela mostra as probabilidades de
Portanto, para este caso você terá que pegar:
Chegaremos em:
Portanto:
E assim para cada fucking intervalo....
Eu sei! Mas repara o seguinte, você vai precisar fazer só até:
Aproximando pela normal:
Mas por que?? Porque a partir disso os valores vão começar a se repetir... olha na tabelinha abaixo como fica:
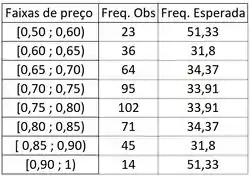
Percebeu? Já é uma ajuda né?!
Passo 3
Agora, vamos definir nossa região crítica:
Vamos ter de buscar na tabela de distribuição qui-quadrado, um valor , tal que:
Uma observação muito importante.... a partir de agora só vamos usar a tabela Qui-quadrado; esquece a tabela Normal agora; usamos ela só para encontrar as frequencias esperadas. BLZ?
Para achar o mininu vamos ter de olhar na coluna que representa 5% e na linha que nos da graus de liberdade.
Eita!! Por que??
O certo seria só , né!? Mas acontece o seguinte, você reparou que tivemos que estimar dois parâmetros para realizar o teste?? O Enunciado não nos deu nem , tivemos que tirar da cartola...aí toda vez que isso acontece, retiramos um grau de liberdade.
Então como tivemos que estimar dois parâmetros, usaremos
Buscando na tabela então:
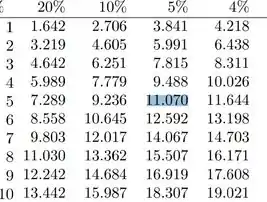
Ou seja, nossa RC terá a seguinte forma:
Bom, agora só falta encontrar o diaxo daquele , bora lá:
Se estivermos certos esses caras erraram feio o modelo em!
Mas é isso então, como pertence e pertence muito à nossa RC, devemos rejeitar a hipótese nula.
Resposta
Concluímos que existem evidências de que o modelo normal não é, nem de perto, o modelo adequado para estudar o preço unitário das mudas.