Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 3.Exercícios - Ex. 144

A variável aleatória X tem a seguinte distribuição de probabilidade.

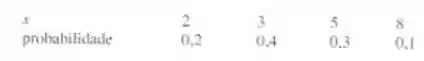
Determine o seguinte:

  1. P ( X ≤ 3 )
  2. P ( X < 2.5 )
  3. P ( 2.7 < X < 5.1 )
  4. E ( X )
  5. V ( X )

Passo 1

Vamos calcular todas as probabilidades direto da tabela que ele dá no exercício!

Letra a:

P ( X ≤ 3 ) = f ( 2 ) + f ( 3 ) = 0.2 + 0.4 = 0.6

Passo 2

Letra b:

P ( X > 2.5 ) = f ( 3 ) + f ( 5 ) + f ( 8 ) = 0.4 + 0.3 + 0.1 = 0.8

Passo 3

Letra c:

P ( 2.7 < X < 5.1 ) = f ( 3 ) + f ( 5 ) = 0.4 + 0.3 = 0.7

Passo 4

Letra d:

E ( X ) = 2 × 0.2 + 3 × 0.4 + 5 × 0.3 + 8 × 0.1 = 3.9

Passo 5

Letra e:

E ( X 2 ) = 4 × 0.2 + 9 × 0.4 + 25 × 0.3 + 64 × 0.1 = 18.3

V a r ( X ) = 18.3 - 3 . 9 2 = 3.09

Resposta

  1. 0.6
  2. 0.8
  3. 0.7
  4. 3.9
  5. 3.09
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma indústria de automóveis está preocupada comuma falha no mecanismo dos freios de determinado modelo. Essa falha pode, em raras ocasiões, causar uma catástrofe em uma rodovia. A distribuição do núme
Administradores de hospitais em cidades grandes estão preocupados com os problemas de trânsito nas salas deemergência dos hospitais. Em determinado hospital de umagrande cidade, os funcionários não co
Assumimos que o número de clientes que chegama cada hora em certo posto de serviços automobilísticossegue uma distribuição de Poisson com média X = 7.(a) Calcule a probabilidade de que mais de dez cli
Em certo fio de cobre, sabe-se que, em média,ocorre 1,5 falha por milímetro. Assumindo que o número de falhas seja uma variável aleatória de Poisson, qualé a probabilidade de que não ocorram falhas em
Os buracos em uma estrada podem ser um graveproblema e precisam de constantes reparos. Para um certo tipo de terreno e pista feita de concreto, experiênciaspassadas sugerem uma média de dois buracos p