Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 3.Exercícios - Ex. 48

Referindo-se ao Exercício 3.39, determine

(a) f   ( y   | 2 ) para todos os valores de y.

(b) P   ( Y = 0 |   X = 2   ) .

Passo 1

Falaa, meu querido/minha querida. No Exercício 3.39 nós encontramos a seguinte tabela para a distribuição de probabilidade:

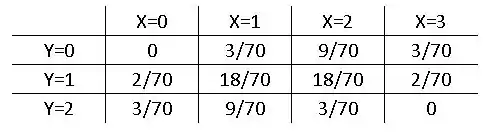
Então, bora para os cálculos!!!

Passo 2

Pela definição de distribuição condicional nós temos:

f y 2 = f ( 2 ,   y ) g ( 2 )

Onde, f ( x ,   y ) é a distribuição de probabilidade conjunta das variáveis aleatórias X e Y , enquanto g ( x ) é a distribuição marginal.

Como g x = ∑ y f ( x ,   y ) , nós encontramos:

g 2 = ∑ y 2 f 2 ,   y = f 2 ,   0 + f 2 ,   1 + f 2 ,   2 = 9 70 + 18 70 + 3 70 = 3 7

Usando isso e a tabela do Passo 1, concluímos:

f 0 2 = P Y = 0 X = 2 = f ( 2 ,   0 ) g ( 2 ) = 9 70 3 7 = 3 10

f 1 2 = P Y = 1 X = 2 = f ( 2 ,   1 ) g ( 2 ) = 18 70 3 7 = 3 5

f 2 2 = P Y = 2 X = 2 = f ( 2 ,   2 ) g ( 2 ) = 3 70 3 7 = 1 10

Passo 3

Na letra (a), nós já encontramos o valor solicitado:

P Y = 0 X = 2 = f 0 2 = 3 10

Resposta

Resolução nos passos anteriores.

Exercícios de Livros Relacionados

Um armazém tem atualmente 30 componentes de certo tipo, dos quais 8 são fornecidos pelo fornecedor 1, 10 pelo fornecedor 2 e 12 pelo fornecedor 3. Seis deles serão aleatoriamente selecionados para uma
Seja X número de câmeras digitais Canon vendidas durante uma determinada semana por uma loja. A fmp de X éSessenta por cento de todos os clientes que compram essas câmeras também compram uma garantia
Retorne à situação descrita no Exercício 3. a. Determine a fmp marginal de X 1 e, depois, calcule o número esperado de clientes na fila da caixa expressa. b. Determine a fmp marginal de X 1 . c. Pela
Uma pilha do tipo C está em condição de trabalho com probabilidade 0,7 , enquanto uma pilha do tipo D está em condição de trabalho com probabilidade 0,4. Uma piIha é selecionada aleatoriamente de um c
Sorteiam-se bolas de uma urna que contém inicialmente 20 bolas vermelhas e 10 bolas azuis.(a) Qual é a probabilidade de que todas as bolas vermelhas sejam retiradas antes de todas as azuis?Agora supon