Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 10.Exercícios - Ex. 87

Repita o Exercício 10.85 usando um novo conjunto de dados obtido realizando, de fato, o experimento 256 vezes.

Passo 1

E aí meus amores nessa questãozinha “Pegue o que puder, sem nada a devolver” okay?

Testar

H 0 : a   d i s t r i b u i ç ã o   o b s e r v a d a   p o d e   s e r   a j u s t a d a   p o r   g ( x , 1 / 2 )         x = 1,2 , 3 …

H 1 : a   d i s t r i b u i ç ã o   o b s e r v a d a   n ã o   p o d e   s e r   a j u s t a d a   p o r   g ( x , 1 / 2 )         x = 1,2 , 3 …

O nível de significância especificado é α = 0.05 .

A estatística de teste é dada por

x 2 = ∑ i = 1 8 f i - e i 2 e i

Sob H 0 a estatística de teste x 2 segue a distribuição de x 2 com 8 - 1 = 7 graus de liberdade.

A região crítica é dada como x o b s e r v a d o 2 > x 0.05 , 7 2 onde x 0.05 , 7 2 é o ponto 0.05 superior da distribuição x 2 com 7 graus de liberdade.

Passo 2

Vamos observar que o pmf da distribuição geométrica com parâmetro 1 / 2 é dado como

g x = 1 2 1 - 1 2 x - 1                   x = 1,2 , 3 …

Realizamos o experimento 256 vezes e as frequências observadas, juntamente com as frequências esperadas, são mostradas a seguir

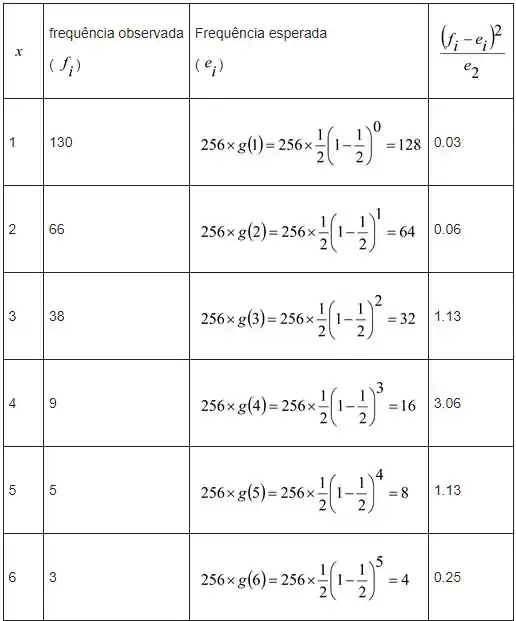
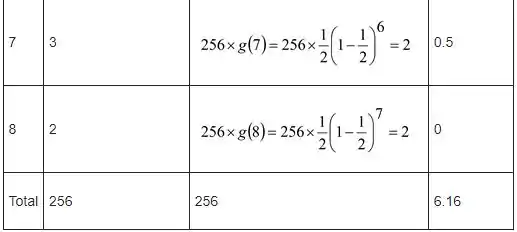
Passo 3

Com os dados temos que x o b s e r v a d o 2 = 6.16

O valor tabelado de x 0.05 , 7 2 é 14.0671

Portanto, x o b s e r v a d o 2 > x 0.05 , 7 2

Portanto, não rejeitamos H 0 , e concluímos que os dados podem ser ajustados pela distribuição geométrica g ( x ; 1 / 2 ) .

Depois dessa questão, “Ninguém se mexe” Meu cérebro caiu.”

Haha bora pra proximaaaa

Resposta

Resposta nos passos.

Exercícios de Livros Relacionados

Um plano de fidelidade de viagens de executivos foi desenvolvido por uma companhia aérea sob a premissa de que 5% de seus clientes atuais se qualificariam para serem membros. Uma amostra aleatória de
O artigo "Statistical Evidence of Discrimination" (J. Amer Stat. Assoc., 1982, p. 773-783) discute o caso do processo jurídico Swain versus Alabama (1965), no qual foi alegado haver discriminação cont
Os cientistas acreditam que os robôs terão papel crucial nas fábricas, nas próximas décadas. Suponha que, em um experimento para determinar se o uso de robôs para fazer cabos de computador é viável, u
Um fabricante de acessórios de encanamento desenvolveu um novo tipo de torneira sem arruela. Seja p = P (uma torneira desse tipo selecionada aleatoriamente ter um vazamento dentro de 2 anos sob uso no
Uma amostra aleatória de 150 doações recentes em certo banco de sangue revela que 82 eram sangue tipo A. Isso sugere que a porcentagem real de doações tipo A é diferente de 40 % , ou seja, a porcentag