Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 3.Exercícios - Ex. 39
De um saco de frutas que contém três laranjas, duas maçãs e três bananas, uma amostra aleatória de quatro frutas é selecionada. Se é o número de laranjas e é número de maçãs, determine
(a) a distribuição de probabilidade conjunta de e ;
(b) , onde é a região dada por .
Passo 1
Falaa, meu querido/minha querida. Como são 3 laranjas e 2 maçãs no saco, e uma amostra de 4 pedaços de fruta está sendo selecionada, sabemos que a variável aleatória pode assumir os valores e , enquanto a variável aleatória assume os valores e
Sendo assim, podemos concluir:
Então, bora finalizar a questão!!!
Passo 2
A primeira probabilidade dessas duas é igual a , já que a amostra do saco contém apenas 3 pedaços de frutas além de maçãs e laranjas, mas a amostra precisa contar 4 pedaços, então é impossível não escolher pelo menos 1 maçã ou laranja.
A outra probabilidade é igual a porque a amostra contém 4 pedaços de fruta, então não pode escolher 2 maçãs e 3 laranjas, totalizando 5 pedaços.
Todas as outras combinações, que as variáveis e são capazes de assumir, são possíveis.
É possível notar que, se a amostra contém laranjas e maçãs, ela também contém bananas. Portanto, o número de maneiras pelas quais laranjas e maçãs podem ser escolhidas na amostra é:
Sabendo que o número total de maneiras que podemos escolher os pedaços de 4 frutas entre 8 é , temos a seguinte fórmula para a probabilidade:
Calculando todas as combinações com a fórmula disposta acima, encontramos a seguinte tabela:
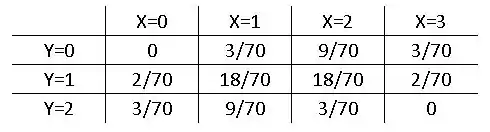
Passo 3
Nós precisamos encontrar a probabilidade , usando a definição de probabilidade conjunta.
Pegando os valores da tabela que montamos acima:
Resposta
(a) Resolução no Passo 2.
(b)