Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 4.Exercícios - Ex. 91

91. As seguintes observações de tempos de falha (milhares de horas) são resultantes de testes de vida aceleradas de 16 chipes de certo tipo de circuito integrado:

82,8 11,6 359,5 502,5 307,8 179,7 242,0 26,5 244,8 304,3 379,1 212,6 229,9 558,9 366,7 204,6

Use os percentis correspondentes da distribuição exponencial com 1 para construir um gráfico de probabilidade. Explique, então, por que o gráfico avalia a plausibilidade da amostra gerada a partir de qualquer distribuição exponencial.

Passo 1

Fala galerinha boa! Tudo bem com vocês? Vamos fazer mais um exercício.

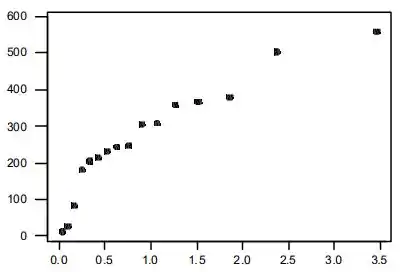
Este gráfico exibe uma curvatura substancial, lançando dúvidas sobre a suposição de uma distribuição populacional exponencial. Como é um parâmetro de escala (assim como para a família normal), = 1 pode ser usado para avaliar a plausibilidade de toda a família exponencial.

Até a próxima, pessoal!

Resposta

No passo 1.

Exercícios de Livros Relacionados

Compare o limite superior da probabilidade P X - E X ≥ 2 V X , obtida pela desigualdade de Tchebycheff, com a probabilidade exata se X for uniformemente distribuída sobre (-1,3).

Suponha que a varável aleatória bidimensional (X,Y) seja uniformemente distribuída sobre R, onde R é definida por x , y x 2 + y 2 ≤ 1 ,y ≥ 0 . (Veja a Fig. 7.17.) Calcule ρ x y , o coeficiente de corr

Suponha que X e Y sejam variáveis aleatórias independentes, cada uma delas uniformemente distribuída sobre (1,2). Seja Z = X Y , obtenha as expressões para E(Z) e V(Z).

Se o lucro de um revendedor, em unidades de $5.000, sobre um novo automóvel pode ser visto como a variável aleatória X, tendo função de densidade f x =2 ( 1 - x ) , 0x1 0 , c a s oc o n t r á r i o á

A função de densidade das medidas codificadas do afastamento das roscas de um ajuste é f x = 4 π ( 1 + x 2 ) , 0x1 0 ,c a s oc o n t r á r i o á Determine o valor esperado de X.