Seja o número de pacotes que estão sendo enviados por um cliente selecionado aleatoriamente em uma determinada empresa de remessas. Suponha que a distribuição de seja como segue:

a. Considere uma amostra aleatória de tamanho (dois clientes) e seja o número médio da amostra de pacotes enviados. Obtenha a distribuição de probabilidades de .

b. Refira-se à parte (a) e calcule .

c. Considere novamente uma amostra aleatória de tamanho , mas agora enfoque a estatística o intervalo da amostra (diferença entre os valores maior e menor na amostra). Obtenha a distribuição de . [Sugestão: calcule o valor de para cada resultado e use as probabilidades da parte (a).]

d. Se uma amostra aleatória de tamanho for selecionada, qual é ? (Sugestão: você não deve listar todos os resultados possíveis, somente aqueles para os quais .)

A média amostral é a soma de todos os valores dividido pelo número de valores.

E a sua probabilidade é o produto das probabilidades associadas aos dois valores.

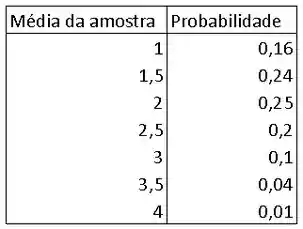
Logo, a distribuição pode ser representada pela tabela abaixo:

Agora, a probabilidade do intervalo amostral é a soma das probabilidades da tabela acima que levam à mesma média amostral.

Então, abaixo temos a distribuição de probabilidade de .

Usando a regra de adição para eventos disjuntos ou mutuamente exclusivos:

Adicionando as probabilidades correspondentes.

Seguindo a mesma lógica do Passo 2, temos:

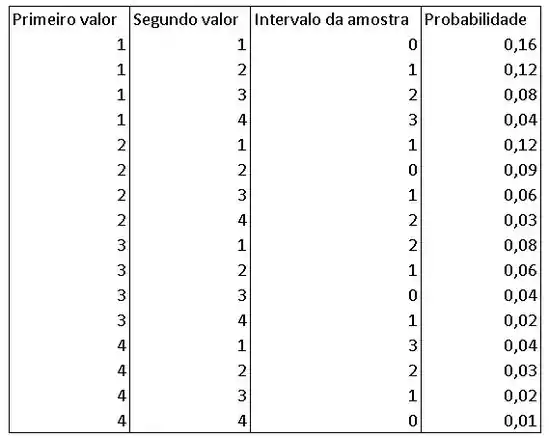
Logo, a distribuição de probabilidade para é:

Amostras de tamanho terão uma média amostral de no máximo , precisa ter as propriedades de que a soma de todos os valores de dados é no máximo 6. Sendo os pontos abaixo:

E a probabilidade dos pontos acima é calculada pelo produto de cada um dos 4 valores:

Sendo assim, a probabilidade quando é a soma das probabilidades acima: