90. Sejam as observações ordenadas da amostra y1 , y2 ,..., yn (y1 sendo o menor e yn o maior). Sugerimos, para verificação de normalidade, que os pares (-1 ((i - 0,5)/n), yi) sejam plotados. Suponha que acreditemos que as observações são provenientes de uma distribuição com média 0 e assuma w1 ,..., wn como os valores absolutos ordenados dos xis. Um gráfico seminormal é um gráfico de probabilidade dos wis. Mais especificamente, como P(|Z| w) = P(-w Z w) = 2 (w) - 1, um gráfico seminormal é um gráfico dos pares (-1 ((i - 0,5)/n) + 1)/2, wi). A virtude desse gráfico é que os pequenos ou grandes outliers na amostra original serão exibidos apenas na extremidade superior e não nas duas extremidades. Construa um gráfico seminormal para a seguinte amostra de erros de medida e comente:
-3,78, -1,27, 1,44, -0,39, 12,38, -43,40, 1,15, -3,96, -2,34, 30,84.
Passo 1
Fala galerinha boa! Tudo bem com vocês? Vamos fazer mais um exercício.
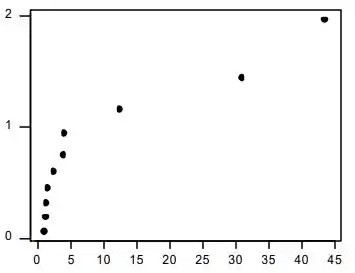
Este gráfico seminormal revela alguns valores extremos, sem os quais a distribuição pode parecer normal.
Até a próxima, pessoal!
Resposta
No passo 1.