Um site da internet de pequenos negócios tem 100 páginas, em que 60%, 30% e 10% das páginas contém baixo, moderado alto conteúdo gráfico, respectivamente. Uma amostra de quatro páginas é selecionada, sem reposição, e X e Y denota o número de páginas com moderada e alta saída gráfica na amostra. Determine

Passo 1
Seja X e Y o número de páginas com gráficos moderados e altos na amostra, respectivamente:
Letra a:
Para calcular a função de massa de probabilidade, observe que em 100 páginas, temos 4, e podemos fazer isso de maneiras. Os resultados que estamos procurando devem satisfazer e . Basicamente, de 30, pegamos x, de 10 pegamos y e do resto, 60, obtemos . Conclusão, a função de massa de probabilidade pode ser calculada como:
Multiplicando as probabilidades, obtemos para cada , para outros a probabilidade é 0. Após o cálculo nós temos:
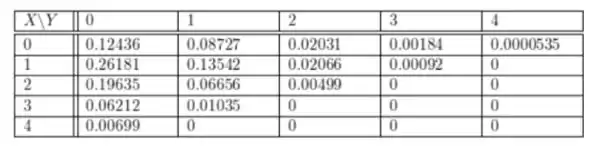
Passo 2
Letra b:
Calculamos a distribuição marginal pela definição:
Que significa que é uma soma das probabilidades em cada linha, ou podemos escrever como:

Passo 3
Letra c:
A expectativa matemática da variável aleatória discreta Y é a soma do produto de cada possibilidade com sua probabilidade :
Usando a definição, nós temos:
Passo 4
Letra d:
Da definição de probabilidade condicional, temos:
onde estão A e B são eventos, e . Podemos calcular para a função de massa também, então nós temos:
onde sabemos que e todos os valores de para cada . Calculando o quociente, obtemos a distribuição, ou a função de massa:
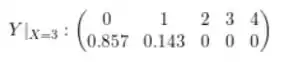
Passo 5
Letra e:
Temos a definição acima, vamos usá-la:
Passo 6
Letra f:
é a variância da variável aleatória X definida como:
Usando a definição da variável aleatória , nós temos:
onde para calcular observe que é uma variável aleatória discreta e que pode ser escrito como nós sabemos que
Passo 7
Letra g:
Podemos encontrar a distribuição marginal para Y e verificar as seguintes funções para cada :
Mas, uma vez que já calculamos , podemos notar que para y = 2:
que não é igual. Conclusão: eles não são independentes.
Resposta
- Ver resolução
- Ver resolução
- 1.2
- Ver resolução
- 0.143
- 0.123
- Não são independentes