Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 4.4 - Ex. 25b
Suponha que a demanda por certa peça, numa loja de autopeças, seguinte modelo:
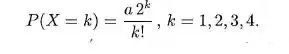
b. Calcule a demanda esperada.
Passo 1
Eai,tudo bem? Bora resolver mais um exercício?
O exercício nos pede para calcular a demanda esperada.
Para isso, vamos construir a tabela abaixo que representa a distribuição de probabilidade de Ok?
Passo 2
Assim,
Vamos calcular a esperança, temos que:
Isso de acordo com os valores da a tabela acima que representa a distribuição de probabilidade de
Resposta
Logo, concluímos o exercício
Exercícios de Livros Relacionados
Numa certa cidade, o número de crianças em idade escolar, em famílias com4 filhos, é uma variável aleatória modelada pela Binomial com parâmetros n =4 e p = 0,6 . Para cada filho em idade escola, um p
Uma peça produzida por uma máquina pode receber do controle de qualidade de três classificações: boa, defeituosa ou recuperável, com as seguintes probabilidades, 0,5 ;0,2 e 0,3 , respectivamente. Supo
Os alunos do curso de estatística têm um time de futebol que não é dos melhores. O cartola que administra o time paga um prêmio de vitória por partida de um sorvete porjogador, acrescentando mais um s
A função de probabilidade da variável X é P X = k = 1 / 5 para k = 1 , 2 , … ,5 . Calcule E ( X ) e E ( X 2 ) e, usando os resultados, determine E [ X + 3 2 ] e V a r 3 X - 2 .
O tempo de duração em horas de uma lâmpada especial foi modelado por uma variável aleatória X com a seguinte função de probabilidade:Cada lâmpada custa ao fabricante R $10 , mas se sua duração for inf