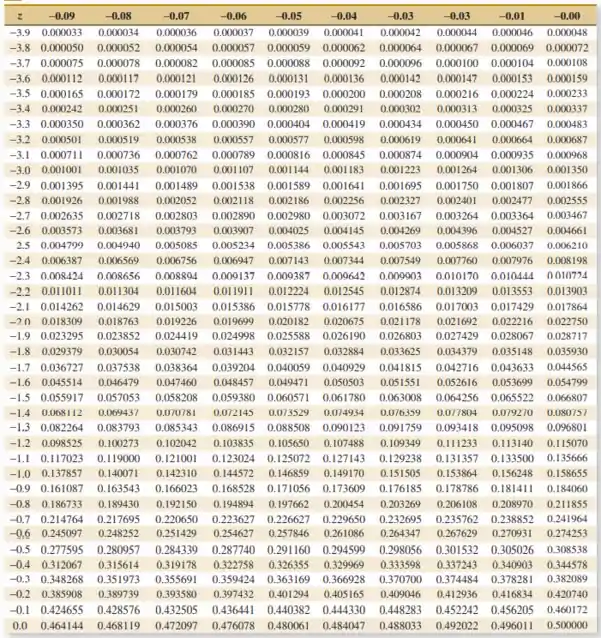
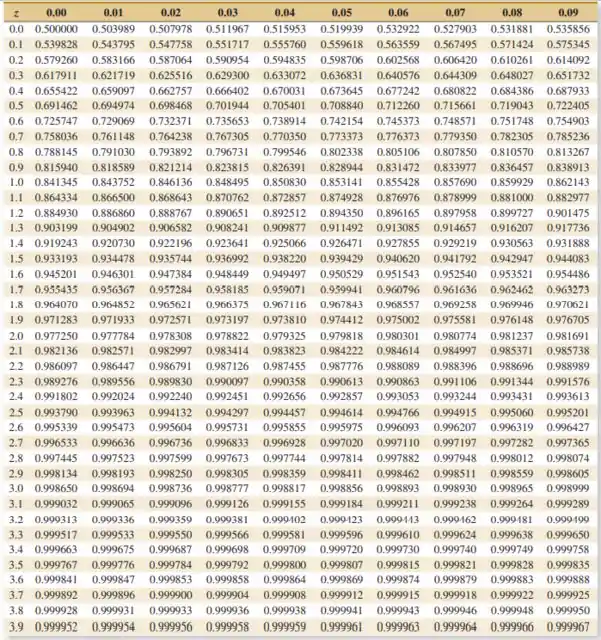
Suponha que tenha uma distribuição normal padrão. Use a Tabela III do Apêndice para determinar o valor de que resolve cada um dos seguintes itens:
Passo 1
Seja a variável aleatória normal padrão com a função de distribuição cumulativa dada nas tabelas dos apêndices do livro.
Primeiro, vamos observar a relação:
Agora, vamos calcular:
Passo 2
Letra a:
É dado que:
que nos leva à:
Usando as tabelas:
Passo 3
Letra b:
Do mesmo modo, obtemos:
Usando as tabelas:
Passo 4
Letra c:
Do mesmo modo, obtemos:
Usando as tabelas:
Passo 5
Letra d:
Do mesmo modo, obtemos:
Usando as tabelas:
Passo 6
Resposta
- 1.96
- 2.58
- 1
- 3