Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 8.Problemas - Ex. 10c
Suponha que e tenham a seguinte distribuição conjunta:
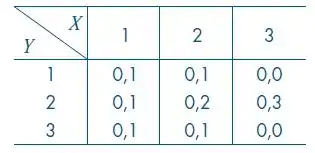
c) Mostre que, embora ), e não são independentes.
Passo 1
Temos que:
Além disso,
Assim,
Entretanto,
Portanto ), mas e não são independentes.
Resposta
Como demonstrado ao norte, E), mas e não são independentes.
Exercícios de Livros Relacionados
Considere o Exercício 4.10. Pode-se dizer que as notas dadas pelos dois especialistas são independentes? Explique.
Um importante sistema age como apoio para um veículo do programa espacial. Um componente único e crucial opera somente 85% do tempo. Para aumentar a confiabilidade no sistema, decidiu-se que três comp
Nos negócios é importante planejar e realizar pesquisas para antecipar o que ocorrerá no final do ano. Pesquisas sugerem que o espectro de lucro (perda) seja o que se segue, com as respectivas probabi
Sabe-se, por meio da coleta de dados e de muitas pesquisas, que o tempo, em segundos, que certo funcionário de uma empresa chega atrasado para o trabalho é a variável aleatória X , com função de densi
O lucro de um revendedor com um novo automóvel, em unidades de $ 5.000, é a variável aleatória X , que tem como função de densidade f x = 2 1 - x , 0 ≤ x ≤ 1 0 , c a s oc o n t r á r i o á (a) Determi