Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Probabilidade Um Curso Introdutório - Dantas- Ed: 3º - Capítulo 3.Exercícios - Ex. 1

Suponha que três bolas são selecionadas ao acaso de uma urna contendo três bola vermelhas, quatro bolas brancas e cinco bolas azuis. Sejam X e Y respectivamente o número de bolas vermelhas e o número de bolas brancas escolhidas. Determine:

a) a distribuição da probabilidade de (X, Y);

b) a distribuição de probabilidade de X e a distribuição de probabilidade de Y;

c) P X = Y .

Passo 1

Fala aí pessoal tudo blz?

Nessa questão sabendo que 3 bolas são selecionadas ao acaso de uma urna que tem: três bolas vermelhas, quatro bolas brancas e cinco bolas azuis, sendo X e Y o número de bolas vermelhas e brancas escolhidas, determine:

a) a distribuição da probabilidade de (X, Y);

b) a distribuição de probabilidade de X e a distribuição de probabilidade de Y;

c) P X = Y .

Relaxa, que essa questão vai ser uma lindeza.

Passo 2

Na letra (a) para encontrarmos a distribuição de probabilidade temos que,

P X = K = r k N - r n - k N n , tendo

X - q u a n t i d a d e   d e   b o l a s   v e r m e l h a s

Y - q u a n t i d a d e   d e   b o l a s   b r a n c a s

Z - q u a n t i d a d e   d e   b o l a s   a z u i s

X , Y ,   Z = 5 - X - Y , com isso temos

P X , Y , Z = X 3 Y 4 Z 5 3 12

P X , Y = X 3 Y 4 5 - X - Y 5 3 12

X + Y ≤ 3

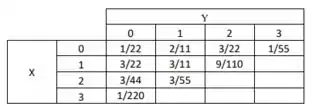
Na letra (b) para acharmos a distribuição de probabilidade em X e Y, temos

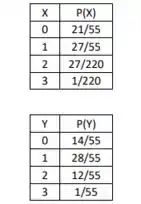
E por fim na letra ( c ) para P X = Y = s o m a   d a   d i a g o n a l , temos

P X = Y = 3 22

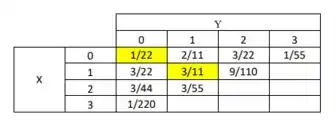
Espero ter ajudado, bons estudos e até a próxima.

Resposta

a)

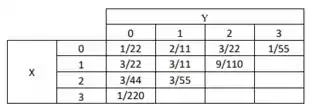
b)

c) P X = Y = 3 22

Exercícios de Livros Relacionados

Uma amostra de 220 clientes de uma clínica dentária foi selecionada. As variáveis tempo, em anos, decorridos desde a última visita ao dentista (V) e o número de cáries encontradas (C) é apresentado na
Na caixa I existem duas bolas numeradas 0 e 1, enquanto que a caixa II contêm duas bolas numeradas 1 e 0. Uma bola é retirada aleatoriamente de cada caixa, de forma independente uma da outra. A esse e
A variável X é Bernoulli com p :0,4 e Y é Binomial com p :0,5en :3 . Admita que XeY são independentes.Determine P X = 0 Y = 2 . Obtenha a função de probabilidade conjunta do X e Y e do produto XY.Calc
A variável X é Bernoulli com p :0,4 e Y é Binomial com p :0,5en :3 . Admita que XeY são independentes.Determine P X = 0 Y = 2 . Obtenha a função de probabilidade conjunta do X e Y e do produto XY.Calc
Na caixa I existem duas bolas numeradas 0 e 1, enquanto que a caixa II contêm duas bolas numeradas 1 e 0. Uma bola é retirada aleatoriamente de cada caixa, de forma independente uma da outra. A esse e