Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 5.3 - Ex. 4b
A tabela de frequência conjunta entre número de filhos (F) e número de casamentos oficiais (C) é apresentada, a seguir, para os 250 funcionários de uma certa empresa.
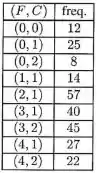
- Determine as tabelas de frequência marginais correspondentes a cada uma das variáveis, isoladamente, e calcule as médias de F e C.
- Construa um gráfico de distribuição de frequência das variáveis. Você chega a alguma conclusão?
- Determine o coeficiente de correlação entre F e C. note que será necessário adaptar a expressão apresentada na Definição 5.4.
Passo 1
Montando o gráfico de distribuição da variável F:
Passo 2
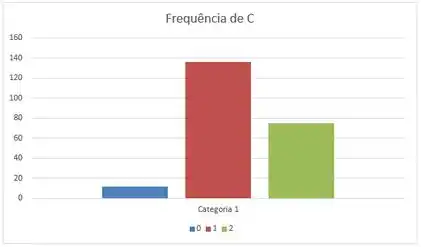
Gráfico de frequência da variável C:
Passo 3
Pelo gráfico de frequência é difícil concluir algo a cerca de ambas as variáveis, somente podemos concluir que a maior parte dos funcionários possui entre 2 e 4, e que a maioria deles teve 2 casamentos oficiais.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Sejam X ~ b 5 ; 0,5 e Y ~ b ( 3 ; 0,2 ) independentes. Determine o valor esperado e a variância da variável 2 X - 3 Y .
Sabe-se que X e Y são independentes e assumem, respectivamente, os valores 1, 2 e 3 e 0, 1 e 2. Admita conhecidas as probabilidades P Y = 0 = 1 3 ,P X = 3 = 1 3 ,P X = 1 ,Y = 0 = 1 9eP X = 3 ,Y = 2 =
Sendo X 1 ,X 2eX 3 variáveis aleatórias independentes, segundo o modelo Bernoulli de parâmetro p, pergunta-se:Qual é a função de probabilidade de X 1 + X 2 + X 3 ? Você reconhece essa variável?Qual é
A conjunta das variáveis aleatórias independentes X e Y é parcialmente apresentada a seguir:Complete a tabela.Calcule o valor esperado e a variância de 2 X - Y .
As variáveis F e M representam, respectivamente, o número de anos para completar o ensino fundamental e o ensino médio. Numa certa idade, a tabela a seguir é adotada para funções de probabilidade conj