Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 5.3 - Ex. 22

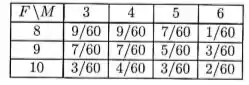
As variáveis F e M representam, respectivamente, o número de anos para completar o ensino fundamental e o ensino médio. Numa certa idade, a tabela a seguir é adotada para funções de probabilidade conjunta dessas variáveis. Determine o valor esperado e a variância da variável F   +   M que representa o total de anos até completar o ensino médio.

Passo 1

Vamos inicialmente montar a função de probabilidade utilizando as marginais, assim:

Além disso, vamos também fazer a tabela F + M , assim:

Passo 2

Temos que, a esperança de F + M será dada por:

E F + M = E F + E M

E, a esperança de uma forma genérica é dada por:

E X = ∑ x ⋅ p x

Assim,

E F = 104 30 + 99 30 + 10 5 = 263 30

E M = 57 60 + 4 3 + 5 4 + 6 10 = 62 15

Logo,

E F + M = 263 30 + 62 15   = 129 10

Passo 3

Já a variância, é dada da seguinte forma:

V a r F + M = V a r F + V a r M

E a variância, de uma forma geral é dada por:

V a r X = E X 2 - E X 2

Assim,

V a r F = 832 30 + 891 30 + 100 5 - 76,85 = 7 12

V a r M = 171 60 + 16 3 + 25 4 + 36 10 - 17,08 = 143 150

Logo,

V a r F + M = 7 12 + 143 150 = 461 300 = 1,54

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que a seguinte função satisfaz as propriedades de uma função de probabilidade conjuntas.Determine o seguinte: f) a distribuição de probabilidade de marginais da variável aleatória X. g) A distr
Suponha que as variáveis aleatoriamente X, Y e Z tenham a seguinte distribuição de probabilidades conjuntasDetermine o seguinte:
O tempo entre os problemas de acabamento de uma superfície em um processo geral de galvanização é exponencialmente distribuído, com uma média de 40 horas. Uma única planta opera três linhas de galvani
Para a marca de referência do Conselho de desempenho do processamento de transação do exercício 5.10, sejam X, Y e Z e o número médio de operações de seleciona, atualizar e insere requerido para cada
A distribuição de probabilidades condicionais de Y, dado que ir a distribuição de probabilidade imaginar a justiça é uma distribuição contínuo uniforme de 0 a 10. Plote para vários valor de X. Determi