Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 5.3 - Ex. 24
A tabela a seguir representa a função de probabilidade conjunta entre o número de empregos desde que começou trabalhar e idade do primeiro emprego , de jovens em uma pequena cidade do Estado de São Paulo.
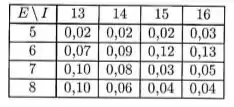
- Determine o valor esperado e a variância da variável
- Idem para
- Obtenha a conjunta entre e .
Passo 1
Em (a) vamos calcular as marginas das variáveis para identificar se elas são independentes e para realizar os cálculos, assim:
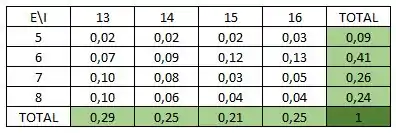
Ao multiplicarmos as marginais relacionadas a uma posição do corpo da tabela, verificamos que o valor não bate, daí, as variáveis não são independentes.
A esperança da variável , será dada por:
De forma geral a esperança é calculada da seguinte forma:
Assim,
Temos que a variância será dada por:
Assim, teremos que a variância será,
Passo 2
Temos em (b) que . Vamos calcular a média de , assim:
Assim, a esperança de será dada por:
Teremos então que a variância será dada por:
Assim,
Passo 3
Fazendo a conjunta de , teremos:
Resposta
Ei, a resposta está no passo a passo :)