Os valores do módulo de elasticidade (MOE, a razão da força, isto é, força por área unitária, para o escoamento, ou seja, deformação por comprimento unitário, em GPa) e a resistência à flexão (uma medida da capacidade de resistência a falhas decorrentes de dobramentos, em MPa) foram determinados para um tipo de amostra de vigas de concreto, gerando os dados a seguir (reproduzidos de um gráfico do artigo “Effects of Aggregates and Microfillers on the Flexural Properties of Concrete”, Magazine of Concrete Research, 1997, p. 81–98):
Passo 1
- Arredonde todos os valores de dados para o inteiro mais próximo.
- O valor de força NÃO é único e totalmente determinado pelo valor de MOE, pois na tabela dada notamos que o valor de MOE de 42,8 corresponde a 2 valores de força diferentes (8,2 e 8,7)
- Equação geral de regressão de mínimos quadrados:
Desenhe uma linha vertical.
Coloque os dígitos das dezenas à esquerda da linha vertical e os dígitos das unidades de cada valor de dados à direita da linha vertical.

Passo 2
A distribuição é assimétrica para a direita (ou assimétrica positiva), porque a maioria dos valores de dados fica perto do topo da tela.
Parece não haver outliers, porque não há lacunas na tela.
O centro parece estar aproximadamente em 41, porque 41 é o valor médio do conjunto de dados classificado.
O spread dos valores está entre 29,8 e 80.
A previsão do intercepto é o valor mencionado na linha com "constante" e na coluna de "Coef" da saída dada:
A previsão da inclinação é o valor mencionado na linha com "mod elas" e na coluna de "Coef" da saída dada:
Substituir na equação de regressão dos mínimos quadrados por 3,2925 e substitua por 0.10748:
Substitua x na equação de regressão por 40 e avalie:
Assim, a resistência prevista é 7,5917 para uma viga cujo módulo de elasticidade é 40.
Não seria apropriado usar a linha de mínimos quadrados para prever a resistência quando o módulo de elasticidade é 100, porque 100 não está dentro da faixa de valores MOE dados (que é chamado de extrapolação)
- Determine os valores previstos para todos os dados valores.
Determine a diferença quadrada entre os valores y observados e a média dos valores y.
Determine a diferença quadrada entre os valores y previstos e a média dos valores y.
Determine a diferença quadrada entre os valores y observados e os valores y previstos.
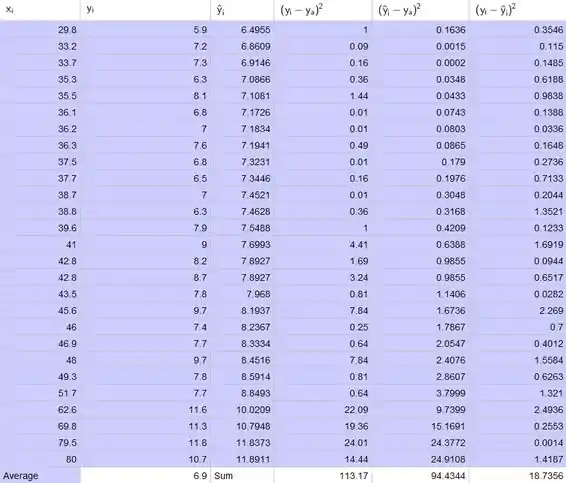
Da tabela temos que:
O coeficiente de determinação é a razão de SSR e SST
Isso significa que 73,83% da variação observada na força pode ser atribuída à relação de regressão linear simples entre as duas variáveis e, portanto, o modelo parece ser um bom modelo.
Resposta
- Inclinado para a direita
- Não