Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 3.1 - Ex. 6

Uma variável aleatória X tem a seguinte função de distribuição:

Determine:

  1. A função de probabilidade de X.
  2. P X ≤ 12 .
  3. P X < 12 .
  4. P 12 ≤ X ≤ 20
  5. P ( X > 18 )

Passo 1

Através da função de distribuição podemos fazer o gráfico dessa variável:

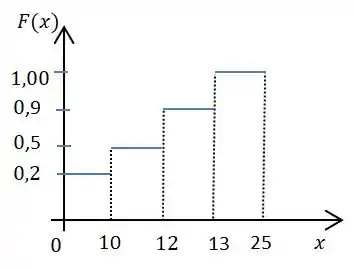
Passo 2

  1. Podemos montar a seguinte tabela a partir do gráfico:

    2. Passo 3

    A partir da consulta da tabela podemos determinar:

  2. P X ≤ 12 = F 12 = 0,5
  3. P ( X < 12 ) = F 10 = 0,2
  4. P 12 ≤ X ≤ 20 = P X ≤ 20 - P X < 12 = F 13 - F 10 = 0,9 - 0,2 = 0,7
  5. P X > 18 = 1 - P X ≤ 18 = 1 - F 18 = 1 - F 13 = 0,1  

Resposta

  1. P X ≤ 12 = F 12 = 0,5
  2. P ( X < 12 ) = F 10 = 0,2
  3. P 12 ≤ X ≤ 20 = P X ≤ 20 - P X < 12 = F 13 - F 10 = 0,9 - 0,2 = 0,7
  4. P X > 18 = 1 - P X ≤ 18 = 1 - F 18 = 1 - F 13 = 0,1  
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando os dados da Tabela 2.1: ( a ) Construa a distribuição de freqüências para a variável idade. ( b ) Faça o gráfico da porcentagem acumulada. ( c ) Usando o gráfico anterior, ache os valores de i
Calcule a variância da v.a. Y definida no Problema 13.
O tempo T, em minutos, necessário para um operário processar certa peça é uma v.a. com a seguinte distribuição de probabilidade.(a) Calcule o tempo médio de processamento.
No problema 1, obtenha as distribuições das v.a. 3X e X².
Para cada peça processada, o operário ganha um fixo de $2,00, mas, se ele processa a peça em menos de seis minutos, ganha $0,50 em cada minuto poupado. Por exemplo, se ele processa a peça em quatro mi