Teste de Hipóteses para comparação entre Médias Populacionais com σ Conhecidos
Teoria
Até agora vimos várias formas de testar um parâmetro de uma população, certo? E agora vamos ver como seriam as coisas se quiséssemos comparar médias de duas populações diferentes! Vamos ver cada caso.
1º caso: Variâncias populacionais conhecidas
Vamos começar no melhor ritmo, já com um exemplo:
“Uma empresa comercializa tintas para pinturas gerais. O engenheiro químico da empresa está interessado em reduzir o tempo de secagem das tintas fabricadas. Para isso, ele resolve coletar dados relativos ao tempo médio de secagem de pinturas feitas com a tinta de fórmula 1, e de outras pinturas feitas com uma nova tinta de fórmula 2. Os resultados encontrados foram:
Sabendo que o tempo de secagem das tintas segue uma distribuição Normal, o empresário pode afirmar que houve uma diferença entre as médias populacionais dessas duas fórmulas? Teste a um . Considere as variâncias populacionais do tempo de secagem das tintas iguais a .”
Agora estamos interessados em testar se duas médias populacionais são diferentes!!! Então vamos ter DUAS populações a serem testadas, e cada uma delas vai ter seu respectivo parâmetro.
A fórmula 1 de tintas vai ter os parâmetros:
E a fórmula 2, da mesma forma, terá os parâmetros:
Já que as duas seguem uma distribuição Normal e tem a variância igual a !
1º Passo)
Como sempre fizemos, nosso primeiro passo é seeempre definir nossas hipóteses. Aqui no teste para diferença entre médias, nossa hipótese nula vai ser SEMPRE essa aqui:
Ou, passando a média 2 pro outro lado...
E a nossa hipótese alternativa, sempre temos que descrever o que está sendo testado e contradizer a hipótese nula. Como aqui queremos testar se há diferença, nossa hipótese alternativa tem que contradizer a igualdade de médias:
Estamos num teste bilateral!
2º Passo)
Agora vamos calcular nossa estatística de teste. No teste para diferença entre médias, ela é dada por:
Onde os e m são os tamanhos das nossas amostras. No nosso exemplo, vimos no enunciado que ambos valem . E as outras incógnitas também conhecemos os valores, que são dados na questão. Substituindo geral aí dentro da equação temos...
3º Passo)
Agora temos que procurar os pontos críticos do nosso teste. Vamos ver quais seriam esses pontos para cada tipo de teste.
Teste bilateral
Nossos pontos críticos continuam sendo:
No nosso caso, como ...
Procurando esse na tabela da Normal, temos que...
Então nossa região crítica vai ser:
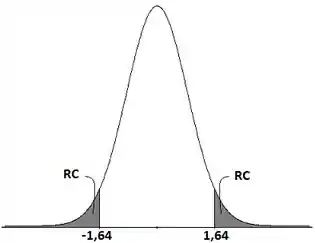
E como nossa estatística de teste cai dentro da RC, nós rejeitamos a hipótese nula!
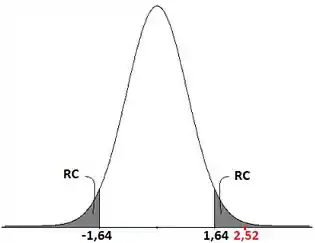
Ou seja, a fórmula 2 para as tintas da empresa realmente modificam o tempo de secagem das pinturas, já que nosso teste provou que as médias são diferentes.
Reparou que a única diferença no teste foi então a estatística de teste e a construção das hipóteses? Os pontos críticos são os mesmos que usávamos no teste de hipóteses para média populacional normalmente!
Então da mesma forma, vamos rever os pontos críticos que usaríamos para os outros tipos de teste.
Teste unilateral inferior
Como estamos no caso INFERIOR, tudo que for MENOR que , será região crítica.
Teste unilateral superior
Como estamos no caso SUPERIOR, tudo que for MAIOR que , será região crítica.
No próximo tópico abordamos os outros casos!
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Uma pessoa que desenvolve produtos está interessada em reduzir o tempo de secagem de um zarcão. Duas formulações de tintas são testadas; a formulação 1 tem uma química padrão e a formulação 2 tem um novo ingrediente para a secagem, que deve reduzir o tempo de secagem. Da experiência, sabe-se que o desvio padrão do tempo da secagem é igual a 8 minutos, e essa variabilidade inerente não deve ser afetada pela adição do novo ingrediente. Dez amostras são pintadas com a formulação 1 e outras dez com a formulação 2. As 20 amostras foram pintadas em uma ordem aleatória.
Os tempos médios de secagem das duas amostras são e , respectivamente. O idealizador de produtos pode afirmar que a eficiência aumentou com o novo ingrediente? Teste usando .
Passo 1
Muito blábláblá nesse enunciado para nos dizer o que?
“...Da experiência, sabe-se que o desvio padrão do tempo da secagem é igual a 8 minutos, e essa variabilidade inerente não deve ser afetada pela adição do novo ingrediente...”
Ele tá nos dizendo que o desvio padrão populacional vale e que ele não muda com a adição do nosso ingrediente, ou seja, é conhecido e, além disso:
E sabendo disso, o enunciado quer saber se a eficiência aumentou com a nova fórmula, ou seja, se nosso tempo de secagem diminuiu.
Então nós estamos num Teste de hipótese para comparação entre duas médias (os tempos de secagem médios!) com conhecidos!
Passo 2
Vamos começar definindo nossas hipóteses. Na nula, sempre igualamos os dois parâmetros que estamos testando:
Na alternativa, como queremos testar se o tempo de secagem diminuiu, vamos ter:
Então estamos num teste unilateral superior!
Passo 3
Calculando a estatatistica de teste:
Passo 4
E como estamos num teste unilateral superior, o ponto crítico vai ser:
Como :
E nossa região crítica é tudo que for MAIOR que isso. Como nossa estatística de teste vale , ela cai dentro da RC!
Ou seja, nós rejeitamos a hipótese nula que dizia que os rendimentos eram iguais, e aceitamos a alternativa que dizia que o tempo de secagem da nova fórmula era menor que o da antiga, ou seja, o rendimento aumentou!
Resposta
Rejeita-se .
Exercício Resolvido #2
Elaboração Própria
Testes de resistência à tensão foram feito com dois tipos diferentes de estrutura de alumínio. Essas estruturas foram usadas na fabricação das asas de um avião comercial. De experiências passadas com o processo de fabricação dessas estruturas e com o procedimento de testes, os desvios padrão das resistências à tensão são considerados conhecidos. Os dados obtidos são os seguintes: , , , , , =1,5.
Se e denotarem as resistências médias verdadeiras à tensão para os dois tipos de estrutura, qual conclusão pode ser tomada a cerca das resistências à tensão das duas estruturas a um ?
Passo 1
Nós precisamos fazer um teste de hipótese para tomar uma conclusão sobre as resistências à tensão das duas estruturas. Então estamos num Teste de hipótese para comparação entre duas médias (as resistências à tensão médias) com conhecidos!
Passo 2
Vamos começar definindo nossas hipóteses. Na nula, sempre igualamos os dois parâmetros que estamos testando:
Na alternativa, como queremos apenas comparar as resistências, e não testar se uma é maior que a outra, vamos ter:
Então estamos num teste bilateral!
Passo 3
Calculando a estatísticas de teste:
Passo 4
E como estamos num teste bilateral, os pontos críticos vão ser:
Como :
E nossa região crítica é tudo que for MAIOR que ou MENOR que . Como nossa estatística de teste vale , ela cai dentro da RC!
Ou seja, nós rejeitamos a hipótese nula que dizia que as resistências eram iguais, e aceitamos a alternativa que dizia que eram diferentes!
Resposta
Rejeita-se .
Exercício Resolvido #3
Elaboração Própria
Um experimento foi realizado para comparar o desgaste de determinados polímeros submetidos a escoamento de fluidos. Foram coletados os seguites dados em duas amostras de dois tipos de polímeros diferentes:
Sabe-se que e .
Ao nível de confiança de , existe diferença nos desgastes médios dos dois polímeros?
Passo 1
Queremos testar se existem diferenças entre duas médias (os desgastes médios!) de dois polímeros. Conhecemos suas variâncias populacionais. Então estamos num caso de Teste de hipótese para comparação entre médias com conhecidos!
Passo 2
Vamos começar definindo nossas hipóteses. Na nula, sempre igualamos os dois parâmetros que estamos testando:
Na alternativa, como queremos verificar se existe diferença:
Então estamos num teste bilateral!
Passo 3
Antes de tudo vamos calcular nossas médias amostrais:
Passo 4
Agora podemos partir para o cálculo da nossa estatística de teste, que nesse caso de teste de hipótese é dada pelo teste Z:
Lembrando que , pois temos cinco elementos nas duas amostras, podemos substituir todos os valores na fórmula e achar a estatística de teste:
Passo 5
Agora podemos calcular nossos pontos críticos, que para o teste bilateral é:
Como o nível de confiança pedido é de :
Então:
E como estamos no teste bilateral, nossa região crítica vai ser tudo que for MENOR que e também tudo que for MAIOR que . O que significa que nossa estatística de teste de cai fora da região crítica, já que ela está entre e . Ou seja, nós não rejeitamos a hipótese nula!
Não podemos afirmar portanto que há diferença entre as médias dos desgastes.
Resposta
Não rejeita-se .