Teste de Hipóteses para comparação entre Médias Populacionais com σ Desconhecidos
Teoria
2º caso: Variâncias populacionais desconhecidas
Agora vamos ter muita calma! Dentro do caso de variâncias populacionais desconhecidas, vamos ter muitos sub-casos. Eles vão ser:
- e desconhecidas e as amostras são maiores ou iguais a .
- e desconhecidas e as amostras são menores que . Nesse caso, vamos ter duas situações:
- Quando .
- Quando .
Vamos ver cada um separadamente.
2.1) e desconhecidas e .
A única diferença desse caso para o caso com variância populacional conhecida vai ser a fórmula da estatística de teste. Quando as variâncias populacionais forem desconhecidas mas as amostras forem maiores que , vamos usar:
Ou seja, a única diferença é que agora vamos usar as variâncias amostrais no lugar das populacionais . A padronização continua sendo a da Normal por que as amostras são suficientemente grandes! Para o resto do teste, seguimos o mesmo passo-a-passo feito anteriormente.
2.2) e desconhecidas, e .
Vamos ver esse caso num exemplo:
“Dois catalisadores estão sendo analisados para determinar como eles afetam o rendimento médio de um processo químico. O catalisador 1 está corretamente em uso, mas o catalisador 2 é aceitável. Uma vez que o catalisador 2 é mais barato, ele deve ser adotado, desde que ele não mude o rendimento do processo. São coletados dados relativos a observações de cada catalizador e os resultados são:
Há alguma diferença entre os rendimentos médios? Use e considere que as variâncias populacionais são desconhecidas, mas iguais.”
1º Passo)
Definir nossas hipóteses:
Já que queremos testar se existe diferença entre as médias, essas seriam nossas hipóteses.
2º Passo)
Calcular a estatística de teste, que agora seria dada por:
Agora vamos passar a usar a padronização T de Student ao invés da Normal, já que estamos num caso de amostras pequenas.
E quem é esse ? Como nossas variâncias populacionais tem valores iguais, apesar de virem de populações diferentes, parece razoável combinar as duas, certo?! Essa combinação é calculada por:
No nosso exemplo, teríamos então:
Então nossa estatística de teste é calculada por:
3º Passo)
E agora, seguindo nossa ordem de seeempre, procuramos os pontos críticos! Vamos ver quais serão eles para cada tipo de teste.
Teste Bilateral
Onde o grau de liberdade . Para o nosso exemplo terímos então:
E como ...
Procurando esses pontos na tabela temos que:
Como nossa estatística de teste , ela cai fora da região crítica:
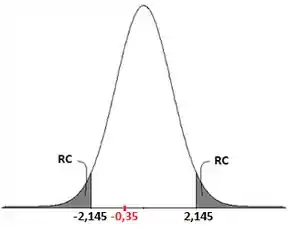
Então nós não rejeitamos a hipótese nula, e podemos dizer que não existem diferenças entre os rendimentos médios dos catalisadores. Vamos ver agora quais seriam os pontos críticos para os outros tipos de testes.
Teste unilateral inferior
Como estamos no caso INFERIOR, tudo que for MENOR que , será região crítica.
Teste unilateral superior
Como estamos no caso SUPERIOR, tudo que for MAIOR que , será região crítica.
Vamos agora ao último caso!
2.3) e desconhecidas, e .
Vamos ver o caso resolvendo um exemplo:
“Um artigo num jornal científico publicou as concentrações de arsênio, em partes por bilhão, na água potável consumina em comunidades de uma região rural, e de outras comunidades da região metropolitana. Foram encontrados os reguintes resultados sobre as duas regiões:
Desejamos determinar se há alguma diferença nas concentrações médias de arsênio entre as comunidades. Teste essa hipótese a um . É improvável que as regiões tenham a mesma variância populacional.”
1º Passo)
Definir nossas hipóteses:
Já que queremos testar se existe diferença entre as médias, essas seriam nossas hipóteses.
2º Passo)
Calcular a estatística de teste, que agora seria dada por:
Agora nossas variâncias amostrais estão entrando separadas aí dentro, reparou? Não temos mais o .
Então nossa estatística de teste é calculada por:
3º Passo)
E por fim, calculamos os famosos pontos críticos. Eles vão ser calculados da mesma forma que para o caso com variâncias iguais, a diferença vai ser o cálculo do grau de liberdade . Vamos ver como fica issaê então!
Estamos em outro teste bilateral, então queremos os pontos:
Porém, como foi dito, agora nosso grau de liberdade é calculado de outra forma, por uma fórmula bem feia inclusive, não se assusta...
Credo, né? Concordo, mas fazer o que... Substituindo os valores do enunciado aí, temos:
Seeeeempre vamos arredondar esse grau de liberdade para BAIXO, para sermos mais conservativos e porque precisamos de um número inteiro como para usar a tabela T.
Então nossos pontos críticos, lembrando que , são...
Procurando na tabela:
Então nosso cai dentro da região crítica:
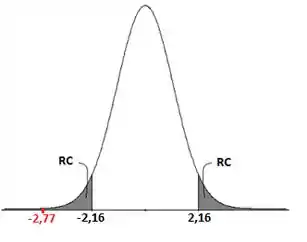
O que significa que rejeitamos a hipótese nula, ou seja, não podemos afirmar que as médias das concentrações são iguais!
Resumindo:
- Se o tamanho da amostra é grande o suficiente, não importa se as variâncias são iguais ou não, fazemos o teste do mesmo jeito que fazíamos para o caso em que as variâncias são conhecidas. Porém, para calcular a estatística de teste, usamos as variâncias amostrais no lugar das populacionais.
- Se a amostra não for grande, usamos a padronização T de Student. Se as variâncias forem iguais, usamos o grau de liberdade tradicional que sempre vinhamos usando. Se as variâncias forem desiguais, usamos aquela fórmula feiosa para o graus de liberdade.
Resumindo:
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Uma empresa realizou um estudo para avaliar o tempo médio de adaptação de funcionários recém formados e funcionários que atuam no mercado há mais tempo. Foram selecionados aleatoriamente: recém formados, obtendo-se tempo médio de adaptação de anos e desvio padrão de anos; funcionários que atuam no mercado há mais tempo, obtendo-se tempo médio de adaptação de anos e desvio padrão de anos.
Teste a hipótese da diferença entre esses tempos médios de adaptação ser nula. Use .
Passo 1
Estamos num caso de teste de hipótese para comparação entre médias com desvio padrôes populacionais desconhecidos, mas temos amostras bem grandes (maiores que 30) então podemos aproximar esse caso para o caso com ’s conhecidos!
Passo 2
Queremos testar se existe diferença entre as médias. Definindo nossas hipóteses:
Então estamos num teste bilateral!
Passo 3
Calculando nossa estatística de teste:
Lembrando que aproximamos para o caso com desvios padrões conhecidos, então a única diferença é que nossos viram na fórmula. Substituindo os valores dados no enunciado:
Passo 4
Agora podemos calcular nosso ponto crítico, que para o bilateral é:
Sabemos que :
Procurando esse cara na tabela da Normal...
E como estamos num teste bilateral, nossa região crítica é tudo que for menor que e tudo que for maior que . Isso significa que nossa estatística de teste , que vale ,
Cai dentro da região crítica! Ou seja, rejeitamos a hipótese nula. =)
Resposta
Rejeita-se .
Exercício Resolvido #2
Elaboração Própria
Uma nova técnica de impressão 3D foi desenvolvida. Para comparar a eficiência entre a técnica tradicional e a nova foi feita a análise amostral de 14 cubos impressos pelo método tradicional (método 1) e de 10 cubos impressos pelo novo método (método 2). Resultando nos seguintes dados:
Ao nível de significância de 5%, podemos afirmar que a diferença nos tempos de secagem das técnicas é maior que ? Assuma que os desvios padrões populacionais são iguais.
Passo 1
Estamos num caso de teste de hipótese para comparação entre médias com desvio padrôes populacionais desconhecidos, porém iguais. Vamos seguir nosso passo a passo pra resolver casos como esse então!
Passo 2
Vamos começar definindo nossas hipóteses. Mas aqui o negócio vai ser um pouquinho diferente do que o que estamos acostumados! Lembra que normalmente escrevemos isso aqui:
Como hipótese nula? E escrever isso aí, nada mais é que escrever:
Correto? Show! Mas aqui nós queremos testar as médias para uma diferença específica. Nós queremos saber se a diferença é maior que . Então nossa hipótese nula teria que ser:
E na alternativa, como queremos verificar se a diferença é realmente maior que , é isso que testamos:
Então estamos num teste unilateral superior!
Passo 3
Mas será que essas hipóteses meio estranhas vai mudar nossa estatística de teste? Quase nada! A única diferença é que temos que subtrair o valor da diferença que estamos testando no numerador da fórmula dela. Se liga só:
Mesma coisa de antes só que com o ali em cima agora. Isso acontece porque na verdade a fórmula “completa” das estatísticas de teste para diferença entre parâmetros sempre inclui o valor da diferença dos parâmetros segundo a hipótese nula:
E como na nossa hipótese nula escrevemos que , nosso fica com o ali no numerador. Nos outros testes que fizemos até agora esse termo não aparece porque sempre estávamos testando com na hipótese nula! Então tínhamos uma subtração zero ali no numerador, que não mudava nada.
Esclarecido esse probleminha, podemos seguir o baile normalmente! Vamos calcular o desvio padrão combinado:
Calculando o :
Passo 4
Agora podemos calcular nosso ponto crítico, que para o teste unilateral superior é:
Sabemos que (pois é pedido 5% de significância). Também sabemos que nosso grau de liberdade é:
Com isso procuramos na tabela:
E tudo que for maior que isso vai ser RC, pois estamos num teste superior. Como vale , nós caímos fora da RC, o que significa que não rejeitamos a hipótese nula!
Resposta
Não rejeita-se .
Exercício Resolvido #3
Elaboração Própria
Des cobaias foram submetidas ao tratamento de ganho de peso com certa ração. Os pesos em gramas, antes e após o teste, são dados segundo a tabela:
A 1% de significância, podemos concluir que a ração contribui para o aumento do peso médio das cobaias?
Passo 1
Precisamos descobrir se o peso médio das cobaias realmente aumentou depois do tratamento, e nós só conhecemos os dados amostrais. Então estamos num teste de hipótese para comparação entre médias (pesos médios!) com desvio padrão desconhecido (já que só conhecemos os dados amostrais, e não os populacionais).
Passo 2
Vamos começar definindo nossas hipóteses. Na nula, sempre igualamos os dois parâmetros que estamos testando:
Na alternativa, como queremos verificar se a média dos pesos aumentou:
Então estamos num teste unilateral inferior!
Passo 3
Antes de tudo vamos calcular nossas médias e desvio padrões. Primeiro para os dados antes da ração:
E agora para os dados depois da ração:
Passo 4
Agora vamos nos situar melhor. Estamos em um teste de hipótese para comparação entre duas médias, com desconhecidos e temos amostras menores que .
Para esse caso, nossa estatística de teste é dada pelo teste T:
Lembrando que , pois temos dez cobaias, podemos substituir todos os valores na fórmula e achar a estatística de teste:
Passo 5
Agora podemos calcular nosso ponto crítico, que para o teste unilateral inferior é:
Sabemos que (pois é pedido 1% de significância), mas falta saber o número de graus de liberdade para procurar esse na tabela. Agora é a hora de usar aquela fórmula feiosa:
Lembrando que sempre arredondamos para baixo para manter o mais conservativo possível. Então nosso
E nossa RC é tudo que for MENOR que isso, já que estamos num teste unilateral inferior. Como nossa estatística de teste deu , ela cai fora da região crítica. Então não rejeitamos a hipótese nula!
Portanto, não podemos afirmar que a ração aumenta o peso das cobais.
Resposta
Não rejeita-se .