Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 13.Problemas - Ex. 3
Uma das maneiras de medir o grau de satisfação dos empregados de uma mesma categoria
quanto à política salarial é por meio do desvio padrão de seus salários. A fábrica A diz ser mais
coerente na política salarial do que a fábrica B. Para verificar essa afirmação, sorteou-se uma
amostra de 10 funcionários não especializados de A, e 15 de B, obtendo-se os desvios padrões
= 1.000 reais e = 1.600 reais. Qual seria a sua conclusão?
Passo 1
Do enunciado:
Considerando:
Duas populações com distribuição normal, independentes e
Para verificar a afirmação da fábrica A devemos testar se a variância dos salários pagos por ela é menor do que a variância da fábrica B; temos portanto um teste de hipótese para a variâncias de duas populações independentes e com distribuição normal:
Passo 2
Teste de Hipótese:
Vamos construir a Região crítica: RC=
Lembrando que, como nossa hipótese alternativa é unilateral inferior, precisamos procurar na tabela o nosso mas a tabela só mostra o unilateral superior(lado direito “>”), portanto para encontrar o precisamos inverter os graus de liberdade do numerador e do denominador, e pegar o inverso do valor encontrado na tabela.
Temos então 0
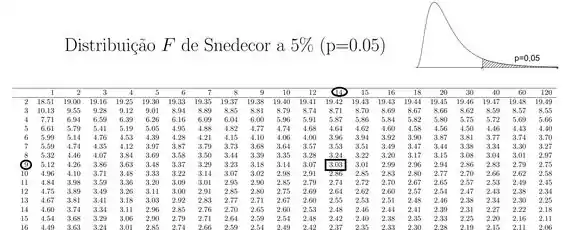
Portanto, nossa região crítica assume a seguinte forma:
Passo 3
Teste sob
Lembrando que o teste sempre é feito sob a hipótese nula, pois ela apresenta a igualdade(
E como definido em
Resposta
Logo, como não pertence à região crítica, não rejeitamos e não há evidencias de que a variância dos salários na fabrica A seja menor do que a variância dos salários na fábrica B.