Teste de Hipóteses para comparação entre Proporções Populacionais
Teoria
E se agora fosse perguntado pra gente algo desse tipo:
“Um pesquisador está estudando os efeitos de um medicamento placebo no tratamento de uma alergia. Para isso, são usadas duas amostras, com pacientes alérgicos cada uma. Os pacientes da primeira amostra recebem o medicamento tradicional que combate a alergia, e é observado que deles melhoram. Os pacientes da segunda amostra recebem o medicamento placebo, e é observado que apenas 19 deles melhoram. Podemos afirmar que existem diferenças entre os resultados dos dois tratamentos? Teste a um ”
A proporção de pacientes da primeira amostra curados é:
E da mesma forma a proporção de curados da segunda amostra é:
E o enunciado pergunta para a gente se podemos afirmar que existem diferenças entre esses resultados de cura.
Reparou que agora está sendo pedido um teste para a difererença entre duas proporções populacionais? Vamos ver como resolve isso então!
Passo 1) Definir nossas hipóteses
Queremos saber se existem diferenças, então:
Aqui não tem muito mistério, todos os testes para diferença entre parâmetros vão seguir esse padrão!
Então estamos num teste bilateral!
Passo 2) Calcular a estatística de teste
Aqui no teste para diferença entre proporções a gente vai usar a padronização da Normal. Mas pera lááá, quem é essa proporção amostral ?! Ela vai ser uma média ponderada das duas proporções que conhecemos:
Substituindo com os valores do nosso exemplo:
Com isso podemos calcular nosso :
Passo 3) Calcular ponto crítico
Vamos ver quais serão os pontos críticos para cada tipo de teste!
Teste bilateral
Como no nosso caso temos :
Procurando esse cara na tabela temos que:
Então podemos ver que nossa estatística de teste cai fora da região crítica:
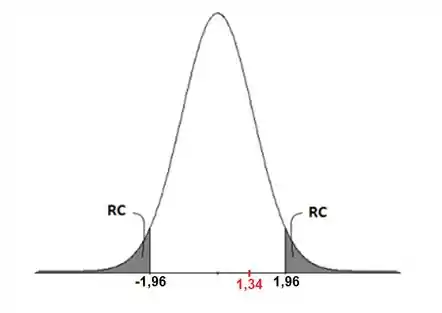
Ou seja, nós não rejeitamos nossa hipótese nula. O que significa que não podemos afirmar que as propoções populacionais dos pacientes que melhoram dos dois tratamentos são DIFERENTES, ou seja, não podemos dizer que o placebo é tão eficiente quanto o tratamento tradicional!
Nossos pontos críticos para os outros tipos de teste seguiriam o mesmo padrão de sempre. Vamos relembrá-los.
Teste unilateral inferior
Como estamos no caso INFERIOR, tudo que for MENOR que , será região crítica.
Teste unilateral superior
Como estamos no caso SUPERIOR, tudo que for MAIOR que , será região crítica.
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Uma associação beneficiente tem adotado dois tipos de pedido de auxílio. No pedido feito por telefone, dos realizados, obteve adesões. Outro tipo de pedido de auxílio, mais dispendioso, teve adesões dentro os contatos realizados. Um dos diretores da associação afirma que o pedido por telefone é mais eficaz. Teste esta afirmação ao nível de significância de .
Passo 1
Queremos verificar se a proporção de adesão pelo telefone é maior que o outro tipo de adesão. Então estamos num teste de hipótese para comparação entre proporções!
Começamos definindo nossas hipóteses:
Vamos chamar de a proporção populacional de adesão pelo telefone, e pelo outro tipo de adesão. Como queremos testar se a por telefone é a mais eficaz (maior), usamos isso aí na hipótese alternativa.
Então estamos num teste unilateral superior!
Passo 2
Vamos começar calculando as proporções amostrais:
Passo 3
Nossa estatística de teste para comparação entre proporções é:
Onde:
Então a estatística de teste fica:
Passo 4
E agora temos que calcular o ponto crítico. Para este tipo de teste ele é dado por:
Como :
E como estamos num teste unilateral superior, tudo que for MAIOR que esse é região crítica. Como a estatística de teste é maior que , caímos na RC!
Isso significa que temos que rejeitar a hipótese nula.
Resposta
Rejeita-se .
Exercício Resolvido #2
Elaboração Própria
Em um estudo de mulheres adultas selecionadas aleatoriamente e homens adultos, ambos usuários de internet, das mulheres e dos homens disseram que planejam comprar online ao menos uma vez no mês seguinte. Ao nível de significância de , testar a afirmação de que há uma diferença entre a proporção de homens e mulheres usuários de internet que planejam comprar online.
Passo 1
Começamos definindo nossas hipóteses:
Vamos chamar de a proporção populacional de mulheres, e a proporção de homens que vai comprar online. Como queremos testar se há diferença, o sinal na hipótese alternativa vai ser o .
Então estamos num teste bilateral!
Passo 2
Nossa estatística de teste para comparação entre proporções é:
Onde:
Então a estatística de teste fica:
Passo 3
E agora temos que calcular os pontos críticos. Para este tipo de teste eles são dados por:
Como :
E como estamos num teste bilateral, tudo que estiver entre e é região de aceitação. Como a estatística de teste é menor que , caímos na região crítica!
Isso significa que temos que rejeitar a hipótese nula.
Resposta
Rejeita-se .
Exercício Resolvido #3
Elaboração Própria
Um fabricante quer testar um novo método de produção de memória RAM. Para isso, ele fabricou memórias pelo método tradicional, e delas foram defeituosas, e memórias pelo método novo e delas foram defeituosas. Teste a um nível de significância de se vale a pena para o fabricante adotar o novo método.
Passo 1
Começamos definindo nossas hipóteses:
Vamos chamar de a proporção populacional de peças defeituosas fabricadas pelo método tradicional, e as fabricadas pelo método novo. Como queremos testar se vale a pena adotar o novo método, queremos testar se a proporção de defeituosas é menor para o novo método, então o sinal na hipótese alternativa vai ser o .
Isso significa que estamos num teste unilateral superior!
Passo 2
Primeiro calculamos nossas proporções amostrais:
Primeiro calculamos nossas proporções amostrais:
Nossa estatística de teste para comparação entre proporções é:
Onde:
Então a estatística de teste fica:
Passo 3
E agora temos que calcular o ponto crítico. Para este tipo de teste ele são dados por:
Como :
E como estamos num teste unilateral superior, tudo que estiver entre for maior que esse ponto crítico é a região de crítica. Como a estatística de teste deu 0, ela cai na região de aceitação!
Isso significa que não podemos rejeitar a hipótese nula.
Resposta
Não rejeita-se .