Teste de Hipóteses para Média Populacional com σ Conhecido
Teoria
Cara, eu te contei lá no tópico de introdução o que era um teste de hipótese e pra que ele serve. Além disso, também disse que ia te ensinar mais pra frente como você ia resolver um, certo? Então, essa hora finalmente chegou!
Calma, prometo que se você curtir essa matéria, eu te pago um sorvete, beleza?
Vamos começar vendo como resolver um teste de hipóteses para média, com nosso querido desvio-padrão conhecido.
Vou te ensinar o passo a passo com um exemplo, que assim você já começa ficando craque no assunto! Vamo lá?!
“Um processo deveria produzir bancadas com de altura. O engenheiro desconfia que as bancadas que estão sendo produzidas são diferentes que o especificado. Uma amostra de valores foi coletada e indicou . Sabendo que o desvio-padrão é , teste a hipótese do engenheiro usando um nível de significância .”
1º Passo) Cara, o primeiro passo vai sersemprecomeçar vendo quem é nosso parâmetro.
Lendo bem o enunciado, a gente percebe que esse engenheiro tá querendo testar a média das alturas dessa bancada, ou seja, nosso parâmetro é o .
Depois disso, vamos escrever quais são nossas hipóteses:
O enunciado fala que a altura deveria ser de , então nossa hipótese nula vai conter essa igualdade.
Como a hipótese alternativa precisa contrariar , e o enunciado não falou nada sobre o cara desconfiar que a altura é menor ou maior que isso, vamos considerar que a média é diferente de .
Estamos em um teste de hipótese bilateral!
2º Passo) Calcular nossa estatística de teste.
Cara, essa estatística de teste é o que vamos usar pra tomar nossa decisão.
Como estamos em um caso de média com desvio-padrão conhecido, a gente pode considerar que estamos num caso de distribuição normal. Isso acontece lááá pelo nosso querido Teorema Central do Limite.
Então, lembra lá da nossa padronização da normal? Vamos usar ela aqui! A fórmula pra calcular a estatística de teste no caso de um teste de hipótese para média com conhecido vai ser:
Vamos substituir com os valores do enunciado?
Guarda esse valor, ele é precioso! E claro, vem comigo pro próximo passo.
3º Passo)Agora precisamos descobrir qual é nossa região crítica.
Só relembrando: a região crítica é a região onde rejeitamos.
Cara, nossa região crítica vai depender do tipo de teste que estamos.
Vamos ter 3 tipos:
Unilateral inferior
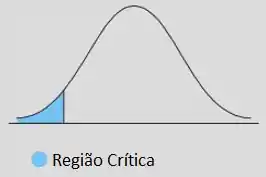
Bom, pra definir onde começa nossa região crítica, precisamos de um valor, certo?
Esse valor vai ser o nosso querido -! Mas que isso?!
Esse valor, que chamaremos de ponto crítico, a gente vai encontrar lá na nossa tabela normal.
Nesse nosso exemplo, como temos , teríamos o seguinte:
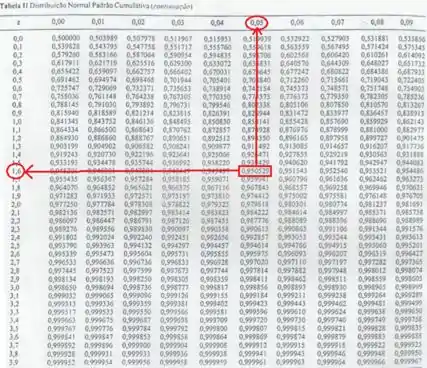
É basicamente ir na tabela normal e ver qual valor de nos dá a probabilidade !
Logo, teríamos:
Unilateral Superior
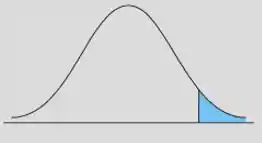
Aqui nosso ponto crítico vai ser bem parecido com o de cima, só que com o sinal oposto!
Vamos ter que procurar o .
Bilateral
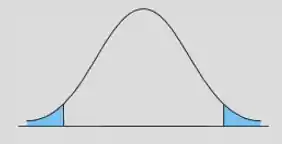
Jááá no caso bilateral, vamos ter dois pontos críticos! Mas calma, não é por isso que é mais difícil não!
Nossos pontos críticos vão ser os seguintes:
Não esquece de dividir o por dois, por favor! E o resto do procedimento é o mesmo dos anteriores.
Bom, voltando pro nosso exemplo...
Vamos descobrir nossos pontos críticos, já que estamos num caso bilateral:
Vamos ver como isso fica no nosso desenho? Lembrando que estamos num caso da distribuição normal, então podemos trabalhar com a nossa querida curvinha.
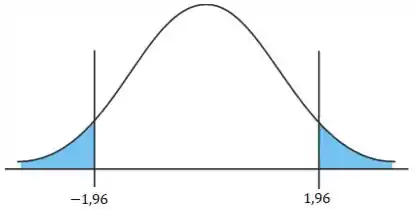
Essa dica é bem valiosa, hein: sempre faça o desenho!
4º Passo) Olhar onde o valor da estatística de teste está no desenho.
Cara, aqui vamos ver se nosso está dentro ou fora da região crítica.
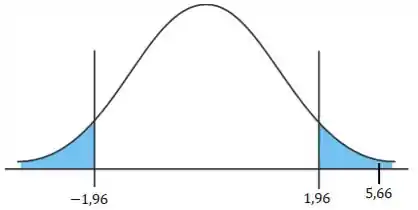
Opa! Nossa estatística de teste está dentro da região crítica. E a região crítica é onde rejeitamos!
5º Passo) Tomar a decisão
Cara, como nosso valor de caiu dentro da região crítica, rejeitamos nossa hipótese nula ! Ou seja, a média de altura das cadeiras é realmente diferente de .
Tranquilo até aqui?!
Resumo
Cara, vou escrever aqui pra você o passo a passo de como resolver um teste de hipótese, pra você ficar bem de boa com isso. Vem comigo!
1º) Identificar o parâmetro e formular as hipóteses, nula e alternativa;
2º)Determinar o valor da estatística de teste;
3º)Descobrir a região crítica;
4º)Ver se a estatística de teste está dentro ou fora da região crítica;
5º)De acordo com o passo anterior, aceitar ou rejeitar .
Não esquece disso não, hein!
Resumo
Exercícios Resolvidos
Exercício Resolvido #1
João Ismael D. Pinheiro, Probabilidade e Estatística: Quantificando a incerteza, Rio de Janeiro: Elsevier Editora Ltda, 2012, pp. 372.
A duração da carga das baterias recarregáveis de notebooks de uma certa marca pode ser encarada como uma variável aleatória com distribuição Normal de média 180 minutos e desvio padrão de 40 minutos. Existe uma falsificação do mesmo produto quase perfeita, mas nesse caso a duração da carga da bateria é uma variável aleatória com distribuição Normal de média 150 minutos e o mesmo desvio padrão anterior. Um montador de notebooks recebe 25 baterias dessa marca. Entretanto, ele tem dúvidas quanto à precedência das baterias. Como ele poderia decidir se as baterias são originais ou falsificadas? Fixe .
Passo 1
Bom, pra gente ver o que ele poderia decidir a gente tem que saber qual será a região de aceitação e a região crítica da hipótese nula, achar o valor de corte. Pra isso, a gente segue aquela rotina lá até o passo que a gente acha essas paradas.
Primeiro definimos e .
Temos que .
Passo 2
Qual é a nossa estatística de teste?
Concorda? Pois é um teste pra média populacional e a gente conhece o desvio padrão populacional.
A gente sabe que a região de rejeição para esse caso é: .
Passo 3
Pra gente achar o de corte é só a gente fazer então:
Vamos achar o valor de corte.
Passo 4
A região de rejeição é então e a de aceitação é .
Com isso podemos dizer que ele deveria rejeitar se , caso contrário, deveria aceitar .
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Teste de Hipótese
O Recursos Humanos de uma dada companhia afirma que o salário médio de uma dada região é de . Para testar esta hipótese, retirou-se uma amostra de trabalhadores desta região e obteve-se um salário médio de e desvio padrão de . Determinar se a hipótese é aceitável a um nível de significância de .
Passo 1
Bom, pra gente ver o que ele poderia decidir a gente tem que saber qual será a região de aceitação e a região crítica da hipótese nula, achar o valor de corte. Pra isso, a gente segue aquela rotina lá até o passo que a gente acha essas paradas.
Primeiro definimos e .
Temos que .
Passo 2
Qual é a nossa estatística de teste?
Concorda? Pois é um teste pra média populacional e a gente conhece o desvio padrão populacional.
Passo 3
Como estamos no primeiro caso lá dos nossos três casos:
Temos região crítica:
Olhando na tabela...
Fazendo agora:
Então nosso valor está dentro da região crítica e sendo assim, a hipótese não é aceitável.
Resposta
Exercício Resolvido #3
Teste de Hipóteses
Pretende-se realizar um teste de hipótese de versus com ,
e .
- Aponte a estatística de teste e o critério de decisão (ou seja, as regiões de rejeição e de aceitação) a serem usados.
- Diga, no contexto de teste de hipóteses, o que são: o e o . Determine a para .
- Que decisão deve ser tomada se nesta amostra com 25 elementos.
Passo 1
Levando em consideração que , , .
Determinamos as hipóteses:
Esse é só pra confundir nossa cabeça, pode usar o que nem aprendemos lá na teoria que vai dar no mesmo!
Estariamos no terceiro caso, beleza? O teste unilateral inferior.
Nossa estatística de teste será:
tem distribuição . Podemos usar a tabela da Normal.
Passo 2
Para o caso unilateral inferior, a gente sabe que nosso ponto crítico que vai definir a região crítica é definido por:
Como o dado é :
Usando tabela, . Então nossa região crítica vai ser tudo que for MENOR que , já que estamos num teste unilateral INFERIOR. Ou seja, se:
Caímos na região crítica e rejeitamos a hipótese nula.
Passo 3
Substituindo em para achar para qual média amostral caímos na região de rejeição:
A gente considera que é o valor de corte. A região de rejeição é e a de aceitação é
Passo 4
(b)
A gente sabe que é rejeitar quando é verdadeira e é aceitar quando é falsa.
A é obtida supondo . Esse é o erro de aceitar quando é falsa.
Temos que calcular a probabilidade do novo (de corte) ser maior do que o 9,23 que foi o que a gente encontrou.
Padronizando:
Usando a tabela da Normal:
Passo 5
(c)
Teríamos que .
Como esse valor é menor que 9,23 estaria dentro da região de rejeição.
Então, a decisão seria rejeitar a hipótese .
Resposta
Exercício Resolvido #4
FURG – Prof. Carla Silva da Silva
O responsável pelo controle de qualidade de uma fábrica que vende suco de laranja, supervisiona periodicamente a linha de produção, para verificar se as caixas de suco de laranja estão com a quantidade correta de suco, isto é, verifica se não está ocorrendo sobreenchimento ou subenchimento da caixinha. Em média, o volume das caixas de suco é de litro e o desvio padrão populacional é de litro. Para testar a hipótese de que haja a necessidade de recalibrar a máquina que enche as caixas, foi retirada uma amostra de caixas de suco. A média encontrada foi de litro. Ao nível de significância de , teste as hipóteses e diga sua conclusão.
Passo 1
Primeiro construímos as hipóteses:
É diferente por que queremos testar se existe sobreenchimento ou subenchimento de suco, então estamos num teste bilateral!
Passo 2
Calculamos nossa estatística de teste:
Passo 3
Agora calculamos nossos pontos críticos (lembrando que nosso ), que no teste bilateral são:
Então nossa região crítica é tudo que tá na região azul:
Como nossa estatística de teste que vale está nela, nós rejeitamos a hipótese nula!
Resposta
Rejeita-se .
Exercício Resolvido #5
Elaboração Própria
Funcionários de uma grande firma de contabilidade afirmam que a média dos salários dos contadores é menor que a de seu concorrente, que é . Uma amostra aleatório de contadores da firma mostrou que a média dos salários de . Sabe-se, de estudos anteriores, que o desvio padrão dos salários é de . Teste a afirmação dos funcionários ao nível de de significância.
Passo 1
Primeiro construímos as hipóteses:
É menos por que é isso que os funcionários querem testar, então estamos num teste unilateral inferior!
Passo 2
Calculamos nossa estatística de teste:
Passo 3
Agora calculamos nosso ponto crítico (lembrando que nosso ), que no teste unilateral inferior é:
Fizemos esse arredondamento por que é o mais aproximado de na tabela que usamos! Com esse ponto crítico, temos que nossa região crítica vai ser:
Como nossa estatística de teste tá caindo FORA dessa região aí, nós NÃO rejeitamos a hipótese nula!
Resposta
Não rejeita-se .