Teste de Hipóteses para Média Populacional com σ Desconhecido
Teoria
Meu amigo, no tópico anterior eu te ensinei a resolver um teste de hipótese para média quando o desvio-padrão populacional era conhecido, lembra?
Mas, e se a gente não tivesse nosso ? Ou seja, se ele fosse desconhecido, o que a gente faria?
Cara, aqui vamos ter dois casos, e eu preciso que você tenha bastante atenção nisso.
Caso 1) Quando nosso for desconhecido, mas o tamanho da nossa amostra for maior ou igual a 30 .
Caso 2) Quando nosso for desconhecido, mas o tamanho da nossa amostra for menor que 30 .
Vamos aprender a resolver esses dois casos?
Vou te ensinar o passo a passo com exemplos, que assim você já fica craque no assunto! Vamo lá?!
Caso 1: n 30
“Um fabricante afirma que seus suplementos não contêm mais do que de sódio. Uma amostra de potes de suplemento fornece, em média, de sódio e desvio-padrão de . Sendo o nível de significância de , os dados refutam ou não a afirmação do fabricante?”
1º Passo) Cara, o primeiro passo vai ser sempre começar vendo quem é nosso parâmetro.
Lendo bem o enunciado, a gente percebe que esse fabricante tá falando sobre a média de sódio nos suplementos, ou seja, nosso parâmetro é o .
Depois disso, vamos escrever quais são nossas hipóteses:
O enunciado fala que a quantidade de sódio nos suplementos não é maior do que , então nossa hipótese nula vai conter essa igualdade.
Como a hipótese alternativa precisa contrariar , e precisamos testar se a quantidade de sódio é maior do que a informada pelo fabricante, vamos considerar então média maior que .
Estamos em um teste de hipótese unilateral superior!
2º Passo) Calcular nossa estatística de teste.
Cara, apesar estarmos em um caso de média com desvio-padrão desconhecido, a gente pode considerar que estamos num caso de distribuição normal! Isso acontece lááá pelo nosso querido Teorema Central do Limite, já que temos um .
Nossa estatística de teste vai ser basicamente a mesma do caso com DP conhecido, porém vamos trocar o desvio-padrão populacional pelo amostral !
Vamos substituir com os valores do enunciado?
Guarda esse valor, ele é precioso! E claro, vem comigo pro próximo passo.
3º Passo) Agora precisamos descobrir qual é nossa região crítica.
Só relembrando: a região crítica é a região onde rejeitamos .
Cara, nossa região crítica vai seguir o mesmo passo a passo que fazíamos com conhecido.
Estamos num caso unilateral superior, logo, temos que encontrar .
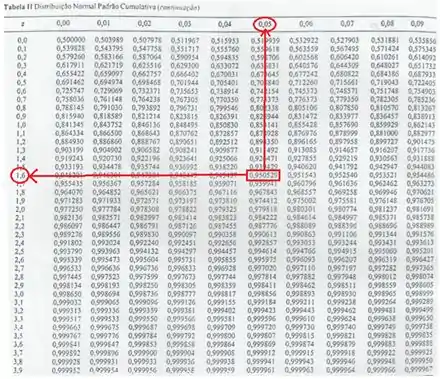
Vamos ver como isso fica no nosso desenho? Lembrando que estamos num caso da distribuição normal, então podemos trabalhar com a nossa querida curvinha.
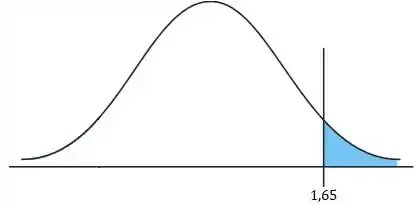
Essa dica é bem valiosa, hein: sempre faça o desenho!
4º Passo) Olhar onde o valor da estatística de teste está no desenho.
Cara, aqui vamos ver se nosso está dentro ou fora da região crítica.
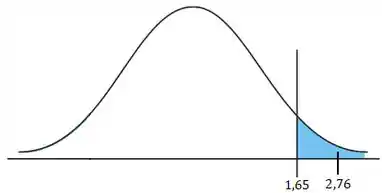
Opa! Nossa estatística de teste está dentro da região crítica. E a região crítica é onde rejeitamos !
5º Passo) Tomar a decisão
Cara, como nosso valor de caiu dentro da região crítica, rejeitamos nossa hipótese nula !
Ou seja, a média de sódio dos suplementos é realmente maior do que . Logo, os dados refutam a afirmação do fabricante.
Até aqui não tivemos muitas mudanças, certo?!
Vamos ver o outro caso!
Caso 2: n 30
“Um trecho de uma rodoviária estadual, quando é utilizado o radar, são verificadas em média 7 infrações diárias por excesso de velocidade. O chefe de polícia acredita que este número pode ter aumentado. Para verificar isso, o radar foi mantido por 10 dias consecutivos. Os resultados foram:
Os dados trazem evidência de aumento nas infrações? Considere ”
1º Passo) Cara, vamos sempre começar vendo quem é nosso parâmetro.
Lendo o enunciado, a gente percebe que ele tá falando sobre a média de infrações diárias, ou seja, nosso parâmetro é o .
Depois disso, vamos escrever quais são nossas hipóteses:
O enunciado fala que a média diária de infrações era , então nossa hipótese nula vai conter essa igualdade.
Como a hipótese alternativa precisa contrariar , e o cara quer testar se a média de infrações aumentou, vamos considerar então média maior que infrações.
Estamos em um teste de hipótese unilateral superior!
2º Passo) Calcular nossa estatística de teste.
Cara, é aqui que vamos começar a notar algumas mudanças. Por ter um , não podemos utilizar a distribuição normal.
Mas relaxa, temos uma outra distribuição muito parecida que vai nos ajudar a resolver nosso problema: a t-student!
O cálculo da nossa estatística de teste vai ser o mesmo do caso anterior, porém vamos trocar o seu nome!
Nem sempre o professor vai ser bonzinho com você, e nesse caso ele não te deu a média e o desvio-padrão amostral. Teríamos que calcular com os dados que ele deu. Mas sem problemas, vamos lá!
Também calculei o desvio-padrão da amostra pra você:
Agora vamos substituir os valores e descobrir nosso valor de .
Guarda esse valor, ele é precioso! E claro, vem comigo pro próximo passo.
3º Passo) Agora precisamos descobrir qual é nossa região crítica, a região onde rejeitamos.
Aqui também vamos ter algumas mudanças, então presta bastante atenção, hein!
Como estamos nessa nova distribuição chamada t-student, teremos uma nova tabela também, bem parecida com a que tínhamos na normal.
Vou analisar cada um dos tipos de teste de hipótese pra você entender direitinho como buscar o valor na tabela.
Unilateral inferior
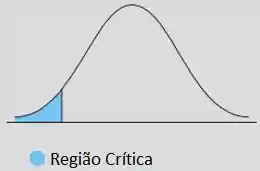
Aqui, o nosso ponto crítico vai ser dado por esse carinha aqui:
Masoquê isso?! Calma, jovem gafanhoto, aqui não tem mistério também!
Esse é o que chamamos de graus de liberdade, e ele vale:
Ou seja, vai ser sempre o tamanho da amostra menos um.
Nesse nosso exemplo, como temos e , teríamos o seguinte:
E a gente vai buscar esse valor na nossa mais nova tabelinha!
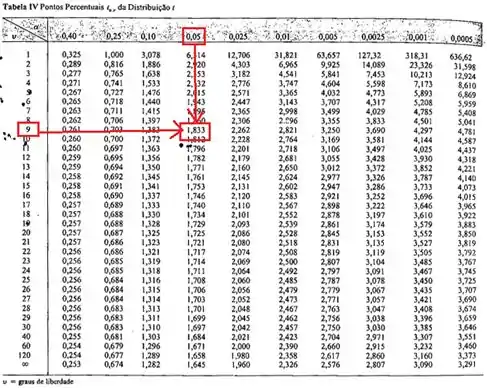
Sem mistérios, viu? Basta cruzar a linha dos graus de liberdade com a coluna do nível de significância .
Lembrando que essa tabela aí tem como parâmetro! Se a sua tabela tiver como parâmetro, você procuraria por na primeira linha.
Unilateral Superior
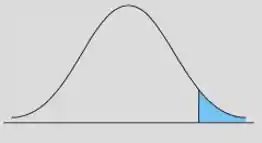
Aqui nosso ponto crítico vai ser bem parecido com o de cima, só que com o sinal oposto!
Vamos ter que procurar o .
Bilateral
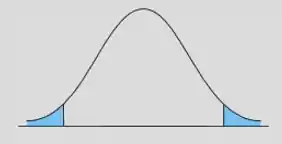
No caso bilateral, vamos ter dois pontos críticos.
Nossos pontos críticos vão ser os seguintes:
Não esquece de dividir o por dois, por favor! E o resto do procedimento é o mesmo dos anteriores.
Bom, voltando pro nosso exemplo...
Vamos descobrir nosso ponto crítico, lembrando que estamos num caso unilateral superior:
Vamos ver como isso fica no nosso desenho? A t-student tem praticamente o mesmo formato da normal, então sem estresse aqui! E não precisa se preocupar, seu professor não vai descontar ponto por achar que você desenhou uma normal, haha.
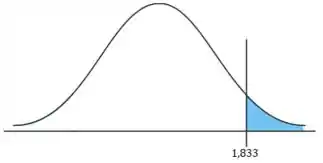
Essa dica é bem valiosa, hein: sempre faça o desenho!
4º Passo) Olhar onde o valor da estatística de teste está no desenho.
Cara, aqui vamos ver se nosso está dentro ou fora da região crítica.
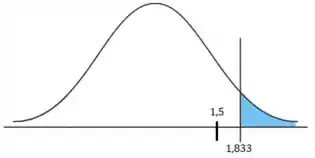
Opa! Nossa estatística de teste está fora da região crítica. Ou seja, ele está na região de aceitação, onde não rejeitamos !
5º Passo) Tomar a decisão
Cara, como nosso valor de caiu fora da região crítica, não rejeitamos nossa hipótese nula !
Ou seja, não houve aumento significativo no número de infrações.
Viu, falei que não era difícil! O passo a passo é o mesmo, só mudando alguns pequenos detalhes. A gente se vê nos exercícios?!
Exercícios Resolvidos
Exercício Resolvido #1
2ª VE – UFF - Teste de Hipóteses
O tempo de duração de um procedimento industrial é de interesse para o fabricante. Uma amostra aleatória de oito procedimentos forneceu e . Há alguma evidência de que o tempo médio do procedimento seja de minutos? .
Passo 1
Bom, temos hipóteses sobre a duração de um procedimento industrial.
Queremos testar a hipótese de que a média é de .
Com isso, vamos cair naquele primeiro caso:
O nível de significância é .
Passo 2
Como não conhecemos o valor de , e sim o de , vamos usar a estatística de teste:
Passo 3
Para esse caso de teste, a região de rejeição é:
Bom, , vamos ter então:
Usando a tabela com graus de liberdade, já que .
Então a região crítica ou de rejeição seria:
A estatística de teste que a gente tem é de:
Com isso, estamos fora da região crítica, isso significa que não há nenhuma evidência contra a afirmação da média ser de .
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
João Ismael D. Pinheiro, Probabilidade e Estatística: Quantificando a incerteza, Rio de Janeiro: Elsevier Editora Ltda, 2012, pp. 388.
Sergio afirma que Raquel dirige seu carro na estrada a uma velocidade média superior a , enquanto Raquel discorda, afirmando dirigir na estrada a uma velocidade média menor ou igual a . Para dirimir essa controvérsia, Sergio resolve cronometrar o tempo (em minutos) que ela gasta ao volante em 10 viagens, sempre pelo mesmo percurso que liga duas cidades 120 distantes:
- Quem parece ter razão, ao nível de significância 5%?
Passo 1
(a)
Primeiro vamos definir as hipóteses:
Temos que .
Na nossa amostra temos . Não conhecemos o valor do desvio padrão populacional, isso é um sinal de que teremos que calcular o amostra e usar .
Passo 2
A nossa estatística de teste será:
E o critério para a região de rejeição será:
Usando a tabela de e levando em consideração que temos graus de liberdade.
Passo 3
Só que para calcular e precisamos antes passar tudo para velocidade, que é sobre o que a questão trata. Foram dados os tempos e a distância, então vamos usar a seguinte fórmula:
Os resultados obtidos em são:
Passo 4
Com base nesses dados a gente pode calcular agora e , usando as fórmulas lá do início da matéria. Vou colocar os resultados direto:
Com isso, temos:
Observando o critério da região de rejeição, como então isso implica que deve ser rejeitada. Ou seja, Sergio parece ter razão.
Resposta
Exercício Resolvido #3
P2- 2013.2 – UFRJ Teste de Hipóteses
Suponha que os tempos de vida, em horas, de certos semicondutores a laser sejam Normalmente distribuidos com média e variância .
Para testar versus , uma amostra aleatória de tamanho 25 foi
observada e apresentou os seguintes resultados:
.
- Qual a sua conclusão, ao nível de significância de 1%?
Passo 1
(a)
Nessa opção a gente vai ter que fazer o teste de hipótese pra esse caso aí com .
Repara que nesse caso a gente não conhece o valor de então teremos algumas diferenças na conta.
Inicialmente, a gente tem:
A nossa estatística de teste vai ser diferente né, porque não temos :
E vamos usar a distribuição com 24 graus de liberdade, já que .
Passo 2
Se liga que esse caso é igual o caso 2 da nossa teoria de teste para média populacional. Para esses casos, a região de rejeição é definida por:
Sabendo que são 24 graus de liberdade, usando a tabela de :
Passo 3
Só que pra calcular o nosso a gente tem que calcular e , usando os dados do exercício e as fórmulas que a gente já conhece.
Como tempo é uma coisa escassa, vou colocar os resultados aqui direto:
Agora podemos calcular o :
Como , então estamos dentro da região de aceitação de .
Resposta
Exercício Resolvido #4
P2- 2012.1 – UFRJ Teste de Hipóteses
Um fabricante de cabos afirma que: “o diâmetro médio dos cabos produzidos pela sua empresa é de pelo menos ”. Para testar se esta afirmação é verdadeira, uma amostra de 25 cabos foi observada e mostrou um diâmetro médio de com um desvio padrão de . Suponha que os diâmetros desses cabos sigam uma distribuição Normal.
- Explicite as hipóteses a serem testadas e apresente a sua conclusão a um nível de significância de 5%. Justifique a sua resposta.
- Com base nos recursos de que você dispõe, determine o intervalo de menor amplitude no qual o -valor se encontra.
Passo 1
(a)
Vamos fazer um teste de hipóteses para a média populacional.
Mas nesse caso a gente não conhece o valor de , conhecemos somente e . Se liga que a gente vai ter usar aqui.
A estatística de teste será:
Passo 2
A região crítica nesse caso é dada por:
O exercício diz que:
Lembrando que são 24 graus de liberdade porque .
Então:
Passo 3
Agora a gente substitui os valores na estatística de teste pra ver no que que dá.
Como esse valor é maior que , então está dentro da região de aceitação. Devemos aceitar, ou pelo menos não descartar, a hipótese .
Passo 4
(b)
Calcular o p-valor.
Se você olhar na tabela na linha dos 24 graus de liberdade, você vai encontrar que:
E,
E o valor que a gente quer tá entre:
Isso leva a gente a:
Então...
Resposta
Exercício Resolvido #5
PUC – 2013.2 – P4 -Teste de Hipóteses
Uma amostra de medidores de participação de manganês numa liga de ferro-manganês apresentou uma média de e desvio padrão de . Assumindo que a participação nominal da média na liga é de .
Pede-se:
- Teste a hipótese ao nível de significância de que a participação de manganês da amostra estudada é superior a . Mostre o resultado através de cálculo e esboce um gráfico da distribuição do teste, indicando a área de rejeição e aceitação com os resultados encontrados.
Passo 1
(a)
A gente tem uma amostra com elementos com:
E vamos fazer um teste de hipótese para a média de participação do manganês na liga.
Primeiro a gente tem que determinar as hipóteses, que pelo enunciado são:
Passo 2
Vamos calcular a nossa estatística de teste...
Como a gente não conhece o desvio padrão populacional , vamos usar o que a gente tem... que é o amostral e usar ...
Passo 3
A região de rejeição pra esse tipo de teste, que se encaixa no caso 2, é:
O foi dado no exercício...
Como temos , então vamos ter graus de liberdade... aí é só olhar na tabela:
A região de rejeição é então:
Passo 4
Como a nossa estatística de teste deu:
E:
Não caímos na região critica, então, aceitamos (dentro desse nível de significância pedido né).
Olha o gráfico aí que representa essa situação...
