Distribuição Geométrica
Produzido por Jorge Alberto NascimentoTeoria
Bora bater um papo sobre distribuição geométrica?
Imagina a seguinte situação: Um jogador de basquete arremessando um lance livre, e eu quero saber a probabilidade do jogador acertar o primeiro lançamento apenas no quarto arremesso
Como que eu faço essa conta?!
Usando distribuição geométrica! 😍
Se liga nesse vídeo abaixo explicando tudo o que você precisa saber sobre distribuição geométrica:
O que que Caracteriza a Distribuição Geométrica
Simples, sempre que a gente quiser que o experimento se repita até que se obtenha um sucesso, usaremos a distribuição geométrica!
Aqui, vamos considerar uma sequência de eventos de Bernoulli, ou seja nos eventos a gente só tem 2 opções. O sucesso e o fracasso, dessa forma:
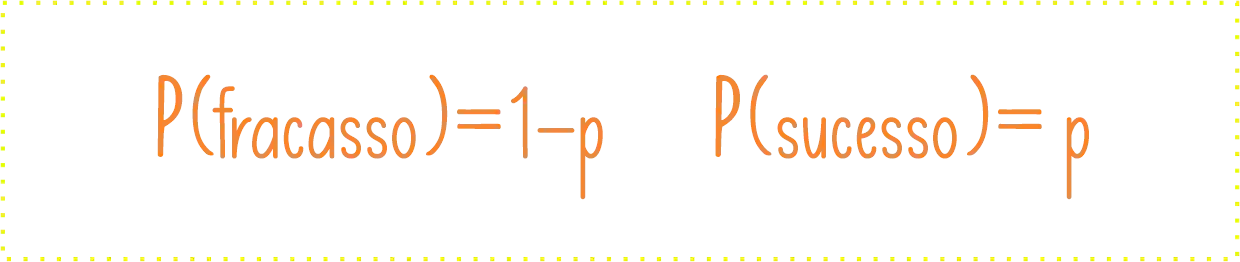
Vamos voltar ao nosso exemplo inicial! Como a gente resolveria? Qual será a probabilidade do jogador acertar o primeiro lançamento apenas no quarto arremesso?
Ai eu vou adicionar mais uma informação, suponha que a gente saiba que a probabilidade do jogador acertar uma cesta é de
Pra início de conversa, vamos da uma olhada no fórmula da função de probabilidade da geométrica:
Onde
Fazendo as continhas:
Prontinho, achamos nossa probabilidade! 🤩
Agora vamos praticar com exercícios?