Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Variáveis Aleatórias Contínuas

Ver Todos os Exercícios

Teoria

Variáveis aleatórias contínuas são variáveis que podem assumir qualquer valor dentro de um intervalo, dessa forma dizemos que ela não pode ser enumerada.

Quando temos um problema em que precisamos fazer um cálculos de probabilidade que envolvem tempo, peso, área e volume usamos variáveis aleatórias contínuas. Isso porque essas variáveis podem assumir uma infinidade de valores! 😉

O Responde Aí preparou um vídeozinho com uma introdução de variáveis aleatórias contínuas

especialmente pra você, da uma conferida! 👇

Ou continua comigo no textinho! 👇

Pra a gente entender melhor quando usamos Variáveis Aleatórias Contínuas eu quero que você pense na seguinte situação:

Um barco carregando óleo sofreu um vazamento no casco e o óleo é derramado. As autoridades Ambientais querem fazer um estudo para tentar estimar a área atingida pelo óleo.

Vazamento de óleo.
Vazamento de óleo.

Podemos criar uma variável aleatória para analisar os possíveis valores para a área afetada.

Mas, você consegue perceber que podemos ter um infinidades de valores para essa área afetada? Para resolver esse tipo de problema utilizamos a variável aleatória contínua.

-Mas porque não uma variável aleatória contínua!?

Diferente da variável aleatória contínua, a variável aleatória discreta só pode assumir um número finito de valores! Sacou?

Função de Densidade de Probabilidade

Pra calcular a probabilidade de um evento com variável contínua a gente vai usar a função de densidade.

A função de densidade descreve a distribuição de uma variável aleatória contínua .

-Hãm? Que? 😵‍💫😵‍💫😵‍💫

Pra você entender melhor, se liga na imagem abaixo:

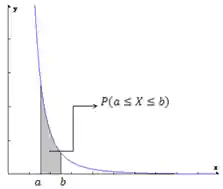
Exemplo: função de densidade
Exemplo: função de densidade

A nossa função de densidade é e a probabilidade de estar entre e é dada pela integral de de até . Sacou?

A gente já vai ver um exemplo mais palpável, mas antes tem algumas coisinhas que você precisa saber sobre função de densidade:

  • para qualquer valor de ;
  • , a área total embaixo da curva é , que é a probabilidade máxima possível.
  • Para qualquer valor de e , , ou seja, a probabilidade do intervalo é igual a área de f(x) diretamente abaixo desse intervalo.

Exemplo - O tempo de vida útil de um equipamento eletrônico de determinado tipo pode ser expresso por uma variável aleatória contínua X, dada pela função de densidade . Determine a probabilidade de que o equipamento dure entre e meses:

Função de densidade
Função de densidade

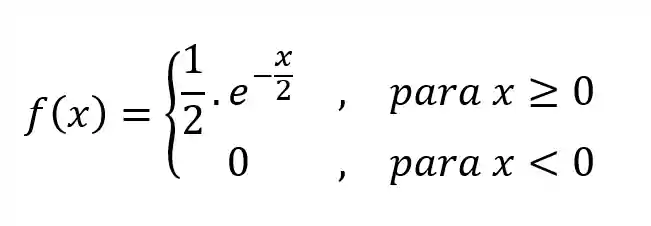
Para resolver esse exemplo antes de mais nada precisamos lembrar que 6 meses é 0,5 anos e que 18 meses são 1,5 anos. Beleza?!

Vamos esboçar a função:

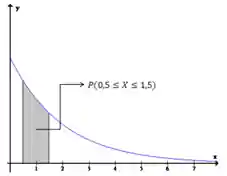
Função de densidade
Função de densidade

Primeiro vamos verificar que a função dada é uma função de densidade, para isso basta verificarmos se:



Beleza?! Se você reparar, temos:

Logo:

Agora podemos calcular a probabilidade pedida:

Show?! Bora praticar com mais exercícios?


Função de Densidade de Probabilidade

Exercícios Resolvidos

Exercício Resolvido #1

Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, -01

Dada a função

f x =   2 e - 2 x , x ≥ 0 0 ,   x < 0

a) Mostre que esta é uma f.d.p.

b) Calcule a probabilidade de x > 10 .

Passo 1

a) Bom, pelo o que vimos na teoria para mostrar que é uma f.d.p. precisamos que a integral dê igual a um certo? Então vamos integrar:

∫ 0 ∞ 2 e - 2 x d x

∫ 0 ∞ 2 e - 2 x d x = 2 × e - 2 x - 2 0 ∞ = 2 × 0 + e - 0 2 = 1

A integral deu 1 entããão mostramos que é uma f.d.p.

Passo 2

b) Queremos agora a probabilidade de x > 10 . Sabemos que:

F ( X ) = ∫ k ∞ 2 e - 2 x d x

Então

P X > 10 = ∫ 10 ∞ 2 e - 2 x   d x = 2 × e - 2 x - 2 10 ∞ = e - 20

Resposta

b) e - 20

Exercício Resolvido #2

7Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 166-02

Uma v.a. X tem a distribuição triangular no intervalo [0,1] se sua f.d.p. for dada por

f x =   0 ,                                         x < 0 C x ,                                                   0 ≤ x ≤ 1 2 C 1 - x ,                           1 2 ≤ x ≤ 1 0 ,                                         x > 1

a) Qual valor deve ter a constante C?

b) Faça o gráfico de f(x)

c) Determine P x ≤ 1 2 ,   P x > 1 2 e   P ( 1 4 ≤ x ≤ 3 4 )

Passo 1

a) Qual valor dever ter a constante C?

De uma coisa nós sempre temos certeza: Se temos uma f.d.p. de uma v.a. contínua, sabemos que a integral no intervalo deve ser igual a um.

Como nesse caso temos quatro intervalos fragmentados, temos que a soma das integrais das funções de cada intervalo deve dar igual a um. Então

∫ - ∞ + ∞ f x d x = ∫ - ∞ 0 0   d x + ∫ 0 1 2 C x   d x + ∫ 1 2 1 C 1 - x + ∫ 1 + ∞ 0   d x = 1

C ∫ 0 1 2 x   d x + C ∫ 1 2 1 1 - x = 1

C × [   x 2 2 0 1 2 + x - x 2 2 1 2 1 ] = 1

C × 1 2 2 2 - 0 2 2 + 1 - 1 2 2 - 1 2 - 1 2 2 2 = 1

C ×   1 8 + 1 2 - 3 8 = 1

C × 2 8 = 1

C = 4

Passo 2

Vamos montar o gráfico agora mas primeiro vamos substituir o C na função:

f x =   0 ,                                         x < 0 4 x ,                                                   0 ≤ x ≤ 1 2 4 1 - x ,                           1 2 ≤ x ≤ 1 0 ,                                         x > 1

Montando as funções por partes

Passo 3

c) Determine P x ≤ 1 2 ,   P x > 1 2 e   P ( 1 4 ≤ x ≤ 3 4 )

Vamos fazer olhando para o gráfico? Já sabemos que a probabilidade é a área do gráfico...

  • P x ≤ 1 2

  •   P x > 1 2

  • P ( 1 4 ≤ x ≤ 3 4 )

Resposta

a) C=4

b)

c) 1 2 ; 1 2 ; 3 4

Exercício Resolvido #3

UFRJ-P1-2012.2-3

O tempo de espera (em minutos) para ser atendido em um sistema de conversa on-line de uma empresa comporta-se de acordo com a seguinte função de densidade

f t = 2 t 3 ,                                                 t ≥ m 0 ,                 c a s o   c o n t r á r i o .

  1. Determine o valor de m .
  2. Calcule a probabilidade de um cliente esperar pelo menos 5 minutos dado que já esperou pelo menos 2 minutos.
  3. O administrador do sistema afirmou que 96% dos usuários esperam no máximo 5 minutos para serem atendidos. Você concorda com o administrador? Justifique a sua resposta.

Passo 1

(a)

Se isso aí é uma função de densidade, a gente sabe que:

∫ m ∞ 2 t 3   d t = 1

- t - 2 m ∞ = 1

m - 2 = 1

1 m 2 = 1

m = 1

Já que não faz sentido ter m negativo.

Passo 2

(b)

O exercício pede uma prob. Condicional P X ≥ 5 X ≥ 2 .

P X ≥ 5 X ≥ 2 = P X ≥ 5 ∩ X ≥ 2 P X ≥ 2

Pela lógica P X ≥ 5 ∩ X ≥ 2 = P ( X ≥ 5 ) , concorda?

A interseção entre a probabilidade de X ser maior ou igual a 5 com X ser maior ou igual a 2, é igual a de X ser maior ou igual a 5, porque tudo que é maior ou igual a 5 também é maior ou igual a 2 e o inverso não é verdade. Enfim, continuando a conta:

P X ≥ 5 X ≥ 2 = P X ≥ 5 P X ≥ 2

Passo 3

P X ≥ 5 = ∫ 5 ∞ 2 t 3   d t

= - t - 2 5 ∞

= 1 25            

Pensando da mesma forma:

P X ≥ 2 = 1 4

Substituindo na fórmula lá:

P X ≥ 5 X ≥ 2 = 1 25 1 4

= 4 25

Passo 4

(c)

O exercício afirma que:

P X ≤ 5 = F 5 = 0,96

A gente sabe que:

P X ≤ 5 = 1 - P X ≥ 5

                    = 1 - 1 25          

= 24 25      

= 0,96

Logo, a gente concorda com o administrador.

Resposta

a   m = 1

b 4 25

c   s i m

Exercício Resolvido #4

Elaboração Própria

Classifique as variáveis abaixo como discretas ou contínuas:

  1. Altura de alunos de uma universidade
  2. Tempo de espera numa fila
  3. Número de idas ao cinema por ano
  4. Quantidade de refrigerante nas latinhas
  5. Quantidade de copas sorteadas num baralho

Passo 1

A altura de um aluno pode ser 1,75 m   por exemplo, certo?

E qual a próxima altura depois dessa? 1,76 m ? Mas por que não 1,759 m ? Ou 1,751 m ?

Reparou que não conseguimos quantificar essas alturas como finitas e sempre vamos poder achar infitas alturas em um intervalo? Por isso, podemos dizer que nossa variável é contínua!

Passo 2

Mesma coisa agora... tempo é o exemplo perfeito de v.a. contínua, por que sempre podemos falar de horas, minutos, segundos, milisegundos, especificando cada vez mais. E isso é infinito!

Então também é uma v.a. contínua.

Passo 3

Quantas vezes podemos ir ao cinema no ano? 5, 8, 10, 15 vezes, sempre algo desse tipo, certo?

Não conseguimos ir, por exemplo, 11,5 vezes. Então nossas idas ao cinema são finitas, e portanto, são discretas!

Passo 4

Quando falamos de massa, tipo a quantidade de refrigerante numa latinha, temos outro exemplo onde as variáveis contínuas são muito mais coerentes. A gente sempre pode especificar cada vez mais a quantidade do refrigerante em questão, e gerar assim infinitos valores válidos para a variável.

Portanto, também é contínua.

Passo 5

Num baralho temos 13 cartas de cada naipe, certo? Então sortear copas num baralho significa que vamos ter de 0 a 13 copas necessariamente, certo?

E entre esse 0 e 13 só vamos ter números inteiros, nada de 4,5 copas.

Então aqui temos uma v.a. discreta!

Resposta

  1. Contínua
  2. Contínua
  3. Discreta
  4. Contínua
  5. Discreta

Exercícios de Livros Relacionados

Suponha que f ( x ) = e - x para 0x .Determine x tal que P ( xX ) = 0.10 Determine x tal que P ( X ≤ x ) = 0.10
Suponha que f ( x ) = e - x para 0x . Determine as seguintes probabilidades: P ( 1X ) P ( 1X2.5 ) P ( X = 3 ) P ( X4 ) P ( 3 ≤ X )
Determine o valor esperado das seguintes variáveis aleatórias:A variável aleatória T definida no Problema 4.6.
Os valores abaixo representam a distribuição de probabilidade de D, a procura diária de um certo produto. Calcula E(D): d : 1 ,2 ,3 ,4 ,5 P D = d : 0,1 ,0,1 ,0,3 ,0,3 ,0,2
Se X for uma variável aleatória contínua, demonstre que P ( x 1 ≤ X ≤ x 2 ) = P ( x 1X ≤ x 2 ) = P ( x 1 ≤ Xx 2 ) = P ( x 1Xx 2 )