Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Produto Vetorial

Ver Teoria
Exercício 1234

Enunciado

Sejam u = 1,1 , 0 ,   v = ( - 1,0 , 2 ) e H = s p a n { 1,1 , 0 , - 1,0 , 2 } . Calcule uma base para o complemento ortogonal de H , usando o produto vetorial. Em seguida determine uma base ortogonal { u - ,   v - ,   w - } de R 3 tal que s p a n u - ,   v - = H .

Passo 1

Primeiramente, como estamos no R 3 , e sabemos que H é um plano, seu complemento ortogonal é uma reta. Assim, basta que façamos o produto vetorial dos geradores de H . Isso irá gerar um vetor perpendicular a esses dois.

w = u × v = i j k 1 1 0 - 1 0 2 = 2 i + 0 ⋅ k + 0 ⋅ j + 1 k - 0 ⋅ i - 2 j ⇒

w = u × v = 2 i - 2 j + 1 k ⇒

w = 2 , - 2,1

H ⊥ = s p a n { 2 , - 2,1 }

Passo 2

Agora, falta calcular uma base ortogonal de R 3 . Uma coisa que podemos fazer é tomar, w = w - , e v = v ¯ , pois já sabemos que eles serão paralelos (um pertence ao complemento ortogonal do outro!). Por fim, fazemos v - × w - = u - . Olhe a figura:

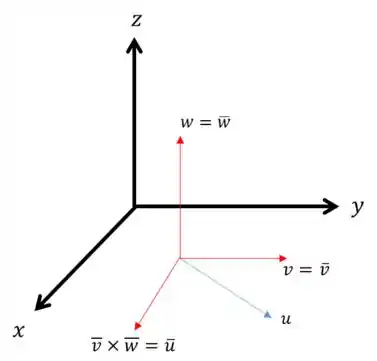
Repare que u - ,   v - ainda pertencem ao mesmo plano de H , e como eles vão ser ortogonais entre si, eles vao ser L I também. E, com isso, podemos dizer que s p a n u - ,   v - = H .

Passo 3

Temos que:

w ¯ = w = 2 , - 2,1

v ¯ = v = - 1,0 , 2

Vamos então calcular u - .

u - = v - × w - = i j k - 1 0 2 2 - 2 1 = 0 i + 4 j + 2 k + 0 k + j + 4 i ⇒

u - = 4 i + 5 j + 2 k ⇒

u - = 4,5 , 2

Assim uma base ortogonal para o R 3 é:

- 1,0 , 2 , 4,5 , 2 ,   2 , - 2,1

E podemos dizer também que:

H = s p a n - 1,0 , 2 , 4,5 , 2

Resposta

H ⊥ = s p a n { 2 , - 2,1 }

Base para o R 3 : - 1 , 0,2 , 4,5 , 2 ,   2 , - 2,1

H = s p a n - 1,0 , 2 , 4,5 , 2