Uma mistura de ar e vapor sofre um processo de saturação adiabática onde a pressão é constante e igual a 100 kPa. Considere que a a temperatura no início do processo seja de 50°C e ao final 25°C. Qual será a umidade absoluta e a umidade relativa no início do processo de saturação? Dado: ;
Passo 1
Para resolver esse problema é fundamental entender que o processo trata de uma saturação adiabática, ou seja, ao final do processo a mistura é uma mistura saturada com isso .
O processo de saturação adiabática tem uma equação governante que é
Vamos analisar termo a termo para entendermos direitinho o que está acontecendo:
- – Umidade absoluta, ou razão de umidade, na entrada.
- – Umidade absoluta, ou razão de umidade, na saída.
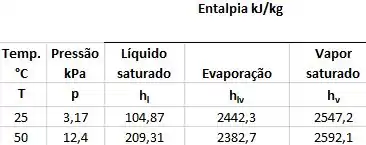
- – Entalpia do vapor na entrada = 2592,1.
- – Entalpia do líquido na saída = 104,87.
- – Entalpia de vaporização na saída = 2442,3.
- – Temperatura no início do processo = 50°C.
- – Temperatura ao final do processo = 25°C.
- – Calor específico a pressão constante da água = 1,0035.
Fora os dados do problema, precisamos de .
Passo 2
Neste passo vamos calcular . Como, ao fim do processo, estamos na saturação também vamos ter que , e a pressão do ar é igual a pressão total menos a pressão do vapor . Com isso a umidade absoluta do final da saturação () p ode ser calculada.
Passo 3
Agora voltamos à equação principal
Passo 4
Vamos achar a umidade relativa e para isso vamos precisar de que vamos calcular agora e que foi dado pela tabela e vale 12,4 kPa.
Para achar nós voltamos à umidade absoluta e meio que fazemos o cálculo inverso, olha só
Como já temos
Viu? Utilizamos a definição da umidade absoluta para achar , obtendo
Passo 5
Substituir na equação da umidade relativa