Rendimento e Pureza
Produzido por Juliana EcheniqueTeoria
Opa, seja bem vindo ao Responde Aí! Bora conversar sobre o Rendimento e Pureza?!
📢 Clique para ver mais:
- Rendimento e Pureza: Exercícios Resolvidos
- Balanceamento e Relações Estequiométricas
- Estequiometria dos Gases
Rendimento de uma Reação
Antes da gente falar o que é rendimento, se liga nessa reação abaixo:
Ela tá balanceada e obedece a uma proporção estequiométrica, ou seja, se a gente reage um mol de
Mais ou menos…. 😖
Pra que seja produzido um mol de
Vamos supor que o rendimento da reação acima seja de
Ou seja, no final teremos
Você também pode assistir esse conteúdo em vídeo:
Pureza dos Reagentes
A pureza de um reagente esta relacionada a sua composição, ela é a porcentagem da substância de interesse presente na amostra. Por exemplo, temos
Pra ficar mais claro, considere a seguinte reação química:
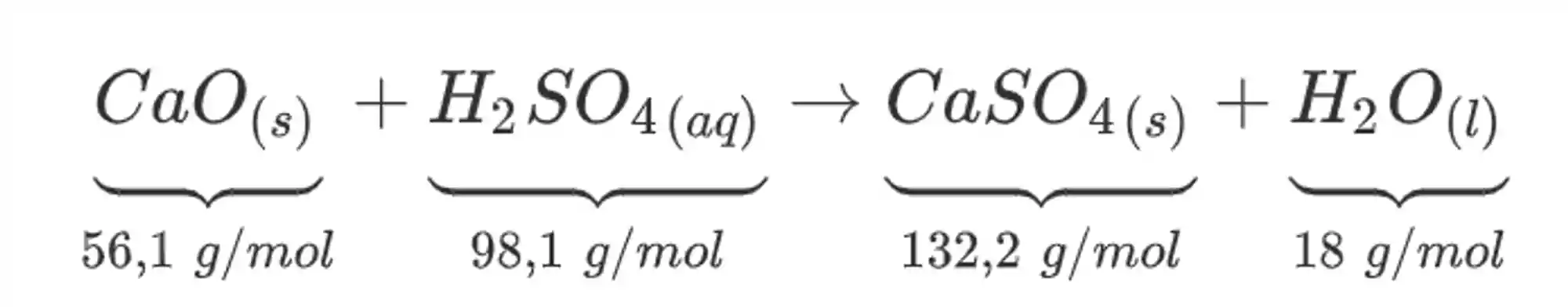
Nessa reação acima consideramos
Nesse caso consumiremos apenas
Reagente Limitante e em Excesso
Como o próprio nome sugere, o reagente limitante limita a reação e se tem um reagente limitante, isso significa que o outro esta em excesso!
Pra ficar mais claro como tudo funciona na prática, imagina a seguinte reação química:
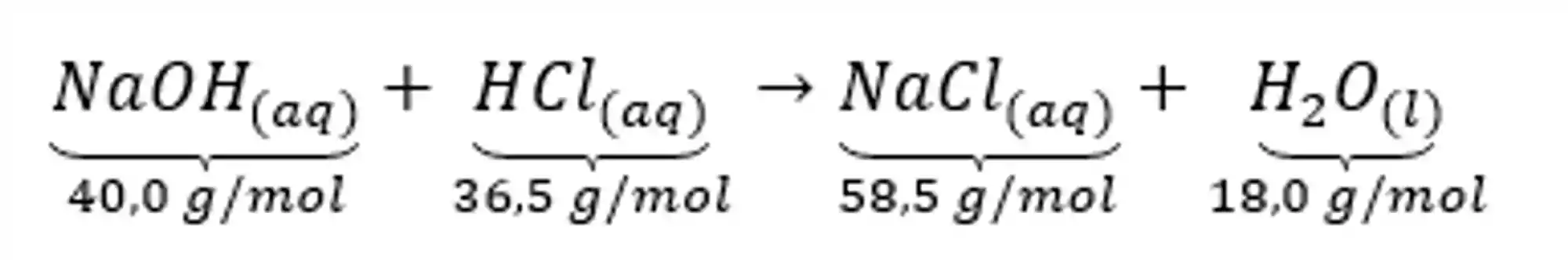
Na figura acima temos as proporções estequimétricas em massa, mas se eu tiver
Pela proporção estequiométrica precisamos de
Prontinho! Agora vamos praticar com exercícios?
Pureza dos Reagentes
Reagente Limitante e em Excesso
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Qual a massa de óxido de cálcio () obtida quando são aquecidos 64 g de calcário () com 80% de pureza?
Passo 1
Primeiro examinamos as realões mássicas entre o óxido de cálcio obtido e o calcário consumido, através da equação química:
Portanto, 56,1 g de são obtidos quando 100 g de são consumidos.
Passo 2
Agora o enunciado nos diz que 64 g de calcário são aquecidos.
Mas se a pureza do material é de 80%, apenas 80% da massa corresponde, realmente, à .
Passo 3
Considerando a relação encontrada no passo 1, calculamos a quantidade de que pode ser produzida com 51,2 g de .

A massa de óxido de cálcio obtida é igual a 28,7 g.
Resposta
28,7 g.
Exercício Resolvido #2
UFRJ/IQ –Prova de Química Geral I – Professor Luiz Fernando Malta. Questão 02.
Considere a reação:
Se 0,86 mol de reage com 48,2 g de , qual é o reagente consumido em primeiro lugar? Quantos gramas de são produzidos?
Passo 1
Pela reação dada (dá aquela conferida rápida pra ver se tá balanceada), 1 mol de reage com 4 mols de .
Então, 0,86 mol de reagem com 3,44 mol de .
A massa molar do é:
Portanto, em 3,44 mol de temos:
Então, precisamos de 125,6 g de pra reagir com 0,86 mol de .
Passo 2
O “reagente consumido em primeiro lugar” é o reagente limitante. Aquele que será consumido por completo, caso a conversão seja de 100 %.
Eaí.. considerando o que calculamos no passo 1, quem é o nosso reagente limitante?
Como precisamos de 125,6 g de pra reagir com 0,86 mol de , mas só temos 48,2 g, temos menos do que o necessário para consumir todo .
O é o reagente limitante. Ele é o reagente consumido em primeiro lugar.
Passo 3
Um erro comum no cálculo do produzido é usar a quantidade de pras relações estequiométricas.
Como o é o reagente limitante, ele é que vai definir quanto de será produzido.
Pela reação, a cada 4 mols de consumidos, produzimos um mol de .
Vamos calcular quantos mols de temos em 48,2 g e, com uma regra de três, ver quantos mol de podemos produzir com isso:
Agora, se 4 mol de produzem 1 mol de , 1,32 mol de produzem:

E como o resultado é pedido em massa:
Portanto, 23,4 g de são produzidos se 0,86 mol de reage com 48,2 g de .
Resposta
23,4 g
Exercício Resolvido #3
UFRJ/IQ –Prova de Química Geral I – Professor Luiz Fernando Malta. Questão 05.
O benzoato de potássio pode ser produzido pela ação do permanganato de potássio sobre o tolueno da seguinte maneira:
Considerando o rendimento percentual de 71%, qual é, em gramas, a quantidade mínima de tolueno necessária para produzir 11,5 g de benzoato de potássio?
Passo 1
Bem, a equação parece balanceada. Então vamos analisar como resolver a questão.
Primeiro, vamos considerar rendimento de 100% e calcular a quantidade necessária para produrir 11,5 g de benzoato de potássio.
Aí, vamos encontrar a massa de tolueno que precisa, de fato, reagir.
Mas como só 71% da massa reage, o valor que encontramos será 71% da massa que vamos usar.
Pra quem gosta de fórmula:
Onde é o rendimento, é a quantidade de reagente que realmente reage e é a quantidade total de reagente.
Bora lá.
Passo 2
Primeiro vamos calcular a massa molar de quem nos interessa:
E pra saber a massa de tolueno que precisamos para formar 11,5 g de benzoato de potássio, fazemos uma regra de três, considerando que 92,1 g de tolueno são necessários para produzir 160,2 g de benzoato de potássio, uma vez que a razão molar entre esses caras é de 1:1.
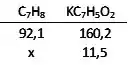
Então, considerando 100% de rendimento, precisaríamos de 6,62 g de tolueno.
Passo 3
Como o rendimento é de 71%:
E a massa de tolueno necessário considerando o rendimento é igual a 9,32 g.
Passo 4
A gente pode conferir nosso resultado fazendo a questão “ao contrário”:
Se tivermos 9,32 g de tolueno reagindo segundo a reação química fornecida, qual seria a massa de benzoato de potássio formada, considerando rendimento de 71%?

Então, com rendimento de 100% formaríamos 16,21 g de benzoato de potássio.
Com rendimento de 71%, a massa obtida será 71% de 16,21:
Ou:
Onde o rendimento é igual a razão entre a quantidade de produto realmente obtida e a quantidade de produto esperada teoricamente ).
Então nosso resultado está certo!
Resposta
9,32 g
Exercício Resolvido #4
UFRJ – Professor Emerson. Lista de Exercícios de Química Geral. Questão 04.
O hidróxido de sódio reage com dióxido de carbono como a seguir:
Qual reagente é o reagente limitante quando 1,70 mol de reage com 1,00 mol de ? Qual é a quantidade de matéria de pode ser produzida? Qual quantidade de matéria do reagente em excesso sobra após a reação se completar?
Passo 1
Pela reação dada, fica claro que 2 moles de reagem com 1 mol de .
Portanto, se temos 1,00 mol de e 1,70 mol de , “falta” pra consumir todo o , e o é o reagente limitante.
Passo 2
Como o é o reagente limitante, ele é que define a quantidade de produto que pode ser produzida. Portanto ele que será usado nos cálculos estequiométricos.
Considerando a massa molar do carbonato de sódio igual a 106,0 g/mol, vemos que:
2 mols de produzem 106,0 g de , tal que 1,70 mol de pode produzir:
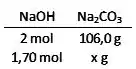
90,1 gramas de .
Para quantidade de matéria em mol:
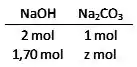
Passo 3
2 moles de consomem 1 mol de , certo?
E queremos saber quantos moles serão consumidos, caso a gente use apenas 1,70 mol de Regra de três!
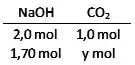
Portanto, ao utilizar 1,70 mol de , vamos consumir 0,85 mol de .
Como, originalmente, tínhamos 1,70 mol de e 1,00 mol de , o xcedente de será:
E 0,15 mol de vão “sobrar” no meio reacional.
Resposta
é o reagente limitante.
90,1 gramas de (0,85 mol) podem ser produzidos.
Sobram 0,15 mol de no meio reacional.
Exercício Resolvido #5
UNIRIO – Lista de Exercícios para P1. Questão 01.
A aspirina, , é preparada pela reação entre o ácido salicílico, , e o anidrido acético, :
a) Que quantidade de ácido salicílico é necessária para preparar kg de aspirina, considerando-se a conversão completa do ácido a aspirina.
b) Considerando o item (a), que quantidade de ácido salicílico seria necessária se o rendimento da reação fosse de 80,0%?
c) Qual a produção teórica de aspirina na reação entre 185 kg de ácido salicílico e 125 kg de anidrido acético?
d) Se na situação descrita na parte (c) forem obtidos 182 kg de aspirina, qual o rendimento percentual da reação?
Passo 1
a) Começa calculando a massa molar do ácido salicíco e da aspirina:
Então, a cada 138,1 g de ácido salicílico, a gente pode produzir 180,2 g de aspirina. Assim, pra produzir kg de aspirina:

Vamos precisar de 114,96 kg de ácido salicílico.
Passo 2
b) Se o rendimento fosse de 80%, para produzir de aspirina, 114,96 seria 80% da massa total de ácido salicíco usada.
Com o rendimento menor que 100%, vamos precisar de mais massa de ácido salicílico!
Você ainda pode calcular pela fórmula:
Ou por regra de três.
![]()
Passo 3
c) Atenção! A gente precisa ver se não existe um reagente limitante!
Então, primeiro vamos analisar a relação mássica existente entre os reagentes:
E por aí que a gente vê que a cada 138,1 g de que reagem, precisamos de .
Portanto, para consumir 185 kg de ácido salicílico ():
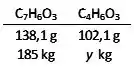
São necessários 136,8 kg de anidrido acético ().
Ao reagir 185 kg de ácido salicílico com 125 kg de anidrido acético, temos menos anidrido do que o necessário para consumir todo o ácido salicílico e, portanto, o anidrido acético será o reagente limitante. Com a massa dele é que vamos calcular a massa produzida de aspirina.
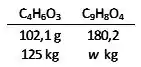
A massa teórica (considerando rendimento de 100%) de aspirina produzida é de 220,62 kg.
Passo 4
d) Se apenas 182 kg fossem obtidos na reação acima, o rendimento poderia se calculado sabendo que 100% corresponde a 220,62 kg de aspirina produzida:

Um rendimento de 82,5% levaria à produção de 182 kg de aspirina.
Resposta
a) 114,96 kg de ácido salicílico.
b) 143,7 kg de ácido salicílico.
c) 220,62 kg de aspirina.
d) 82,5% de rendimento.
Exercício Resolvido #6
Elaboração própria.
Faz-se a reação de 0,150 kg de hidróxido de bário com 0,016 de anidrido sulfúrico (), medidos a Pa.
Considerando a reação abaixo, responda:
a) Qual a substância e sua massa em excesso?
b) Qual a massa de sulfato de bário formado na reação?
Dado:
Passo 1
a) Vamos começar transformando o volume de para gramas:
Observe que as unidades estão coerentes.
O resultado ficou em gramas, uma vez que a gente usou a massa molar em g/mol!
Beleza, então a reação é entre 150 g de e 64,69 g de .
Passo 2
Para determinar qual o reagente está em excesso, precisamos analisar as relações mássicas existentes entre o hidróxido de bário e o anidrido sulfúrico pela reação química.
Sabendo que 171,3 g de hidróxido de bário reagem com 80,0 g de anidrido sulfúrico, podemos calcular a massa de anidrido sulfúrico necessária para reagir com 150 g de hidróxido de bário por regra de três:

Como precisamos de 70,05 g de para reagir com 150 g de , mas só temos 64,69 g, o é o reagente limitante.
Para saber a massa de , em excesso, vamos calcular a massa dele necessária para consumir os 64,69 g de presentes.
Passo 3
Por regra de três:

Como precisamos de 138,52 g de hidróxido de bário e temos 150,00 g, o excesso dessa susbtância é dado por:
Passo 4
Para calcular a massa de sulfato de bário formada, usamos a massa do reagente limitante (64,69 g), ou a massa do reagente em excesso realmente consumida (138,52 g).
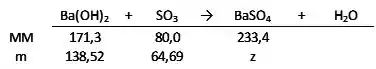
Portanto, 188,7 g de sulfato de bário são formados.
Resposta
a) 11,48 g de hidróxido de bário em excesso.
b) 188,7 g de sulfato de bário.
Exercício Resolvido #7
UNIRIO – Lista de Exercícios para P1. Questão 11.
Os maçaricos funcionam pela reação de combustão do acetileno, , com o oxigênio do ar.
O acetileno é produzido do carbeto de cálcio, com água.
a) Qual o volume de obtido quando 2,0 kg de carbeto de cálcio, com 90% de pureza, reagem com excesso de água a 27°C e 760 mmHg.
b) Determine o reagente limitante e o volume de que será obtido pela reação de 5,00 g de com 100 mL de água nas mesmas condições do item (a).
Passo 1
a) Pela reação de produção do acetileno, vemos que 64,1 g de produzem 26,0g de .
Vamos utilizar 2,0 kg de carbeto de cálcio com 90% de pureza. Portanto, a massa efetiva de carbeto de cálcio será:
Com isso, a massa de acetileno produzida será:
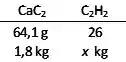
kg
Passo 2
Agora, pela segunda reação:
Vemos que a relação mássica existente entre o acetileno e o dióxido de carbono é dada por:
Ou seja, a cada 26,0 g de acetileno, produzem-se 88,0 g de dióxido de carbono.
Portanto, com os 0,73 kg de acetileno, a massa de produzida será igual a:

Em número de mols, temos:
Passo 3
Para calcular o volume de , consideramos ele como um gás ideal. Sabendo que:
Passo 4
b) Pra resolver o item b, primeiro vamos passar aquele volume de água para número de mol.
Nas condições dadas, a água encontra-se no estado líquido, com densidade aproximadamente igual a 1,0 g/mL.
Portanto, 100 mL de água correspondem a 100 g de água.
O número de mols de água será, então, igual a:
Passo 5
Pela reação abaixo:
1 mol de reage com 2 mols de , logo, 64 g de reagem com 2 mols de .
Se colocarmos 5,00 g de reagindo com 5,56 mols (100 mL) de , teremos excesso de água e o reagente limitante será o .
Com 5,00 g de , a massa de produzida será de:
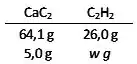
E o número de mols:
Com o qual calculamos o volume:
Resposta
a)
b) Reagente limitante: .
Exercício Resolvido #8
UNIRIO – Lista de Exercícios de Química Geral para P1. Questão 07. Modificado.
Uma das etapas da produção de ferro é a transformação de pirita () em óxido de ferro, como mostra a seguinte reação:
a) Calcule o volume de ar que é necessário para reagir com 100 kg de a 2,5 atm e 250°C. O ar contém 20%, em volume, de .
b) Considerando que a reação 1 teve rendimento de 88% e que todo o dióxido de enxofre foi dissolvido em água, calcule o número de mols de ácido sulfúrico obtido, de acordo com a equação abaixo.
Passo 1
a) Vamos começar calculando a massa molar da pirita e do gás oxigênio:
Considerando que 4 mols de pirita reagem com 11 mols de gás oxigênio, a relação entre as massas que reagem é dada por:
Então 480 g de precisam de 352 g de para reagir.
Portanto, para reagir com 100 kg de , vamos precisar de g de :

Passo 2
A partir da massa de oxigênio, vamos calcular o número de mols de oxigênio necessário para a reação:
E usando a lei dos gases ideais, vamos calcular o volume de gás oxigênio, dadas as condições ( atm e ) e o .
Passo 3
Como queremos saber o volume de ar necessário, sabendo que 20% do ar (em volume) é composto por , podemos calcular:
Ou, por regra de três:
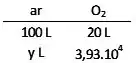
Passo 4
b) Vamos olhar de novo pras relações estequiométricas da reação 1, agora entre a pirita e o formado (você pode usar o ao invés da pirita):
Considerando os coeficientes de cada substância:
Vemos que a cada 480 g de pirita, produziríamos 512 g de , caso o rendimento fosse igual a 100%.
Nesse caso, com 100 kg de pirita:

Considerando que o rendimento é de 88%, apenas 88% dessa massa será realmente produzida.
Ou, pela fórmula:
Onde é a quantidade de produto obtida na prática e é a quantidade de produto esperada teoricamente.
(Obrigado, matemática. Por nos dar sempre o mesmo resultado, independente do “caminho”).
Passo 5
Mas ainda não acabou.
O cara ainda pega esses 93,87 kg de e taca em 10.000 L de água.
Na água, cada mol de forma 1 mol de , segundo:
Considerando as massas molares desses caras:
Com 93,87 kg de , a massa de obtida será de:
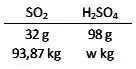
O que, em número de mols, corresponde a:
As relações entre e também podem ser vistas assim:
Como a cada 32 g de consumidos, forma-se 1 mol de :

Resposta
a) 1L de ar.
b) 2,93 mol de ácido sulfúrico.
Exercício Resolvido #9
UNIRIO – Lista de Exercícios para P1. Questão 10.
A amônia, , e o cloreto de hidrogênio, , reagem para formar o cloreto de amônio sólido, .
Dois balões A e B, de 2,00 L cada, a 25°C, são ligados por uma torneira, como mostra a figura abaixo.
Um balão contém 5,00 g de e o outro 5,00 g de . Quando a torneira é aberta, os dois gases reagem até que um deles seja completamente consumido.
a) Que gás resta no sistema depois de a reação ter completado?
b) Qual a pressão final do sistema depois de terminar a reação? (Despreze o volume de cloreto de amônio formado).
Passo 1
a) Primeiro, dadas as massas das substâncias, vamos calcular o número de mols de amônia e cloreto de hidrogênio nos balões.
Como a reação se dá na razão molar de 1:1 (1 mol de reage com 1 mol de ), o está em excesso no meio e restará após a reação ter sido completada.
Passo 2
b) O número de mols de em excesso é dado pela diferença entre o número de mols inicial e aquele necessário para a reação:
E a pressão exercida por esse gás em um recipiente de 4,00 L de volume (ele estará espalhado pelos dois balões) pode ser calculado por:
Sendo:
Portanto:
Resposta
a)
b) 0,92 atm
Exercício Resolvido #10
USP – Lista de Exercícios de Química Geral e Inorgânica 2014. Professor Zeki Naal. Questão 30.
Tratou-se uma mistura de e , pesando 0,560 g com uma solução aquosa de e todo o brometo foi recuperado na forma de 0,970 g de . Qual a fração em peso de existente na amostra primitiva?
Passo 1
Vamos usar a massa de para descobrir o número de mols de , que será igual ao número de na amostra original, uma vez que todo o brometo foi recuperado na forma de .
E fica ligado que o número de mols de brometo é a soma do número de mols de e , afinal foi desses compostos que o saiu.
Passo 2
Pra descobrir o precisamos de mais uma equação, pois temos duas incógnitas e, até agora, só uma equação.
O enunciado nos diz que a massa de mais a massa de é igual a 0,560 g:
E passando essas massas para número de mols:
Substituindo:
Passo 3
Agora a gente tem um sistema pra resolver:
Pra resolver por adição, vamos multiplicar a primeira equação por :
Somando as duas equações, obtemos:
Substituindo na segunda equação:
Passo 4
Agora a gente pode calcular a massa de e assim a porcentagem da amostra que correponde a :
O que corresponde a:
38,4 % da amostra primitiva.
Resposta
38,4 %